2,8 và 3,2 và 3,11 số nào lớn hơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P=\left(-\dfrac{1}{7}\right)^0+\left(-\dfrac{1}{7}\right)^1+\left(-\dfrac{1}{7}\right)^2+...+\left(-\dfrac{1}{7}\right)^{2017}\)
\(\left(-\dfrac{1}{7}\right).P=\left(-\dfrac{1}{7}\right)^1+\left(-\dfrac{1}{7}\right)^2+...+\left(-\dfrac{1}{7}\right)^{2017}+\left(-\dfrac{1}{7}\right)^{2018}\)
\(P-\left(-\dfrac{1}{7}\right)P=\left(-\dfrac{1}{7}\right)^0-\left(-\dfrac{1}{7}\right)^{2018}\)
\(\dfrac{8}{7}P=1-\dfrac{1}{7^{2018}}\)
\(\dfrac{8}{7}P=\dfrac{7^{2018}-1}{7^{2018}}\)
\(P=\dfrac{7^{2018}-1}{8.7^{2017}}\)

\(B=\left(\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1-\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}\right)^2\)
\(=\left(a+2\sqrt{a}+1\right)\left(\dfrac{1}{1+\sqrt{a}}\right)^2\)
\(=\left(\sqrt{a}+1\right)^2.\dfrac{1}{\left(\sqrt{a}+1\right)^2}=1\)
\(C=\dfrac{\sqrt{x}-\sqrt{y}}{xy\sqrt{xy}}:\left[\left(\dfrac{x+y}{xy}\right).\dfrac{1}{\left(\sqrt{x}+\sqrt{y}\right)^2}+\dfrac{2}{\left(\sqrt{x}+\sqrt{y}\right)^3}.\left(\dfrac{\sqrt{x}+\sqrt{y}}{\sqrt{xy}}\right)\right]\)
\(=\dfrac{\sqrt{x}-\sqrt{y}}{xy\sqrt{xy}}:\left[\dfrac{x+y}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}+\dfrac{2}{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)^2}\right]\)
\(=\dfrac{\sqrt{x}-\sqrt{y}}{xy\sqrt{xy}}:\left[\dfrac{x+y}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}+\dfrac{2\sqrt{xy}}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}\right]\)
\(=\dfrac{x-y}{xy\sqrt{xy}}:\left[\dfrac{x+y+2\sqrt{xy}}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}\right]\)
\(=\dfrac{x-y}{xy\sqrt{xy}}:\left[\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}\right]=\dfrac{x-y}{xy\sqrt{xy}}.xy\)
\(=\dfrac{x-y}{\sqrt{xy}}\)
\(=\dfrac{2-\sqrt{3}-\left(2+\sqrt{3}\right)}{\sqrt{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}}=\dfrac{-2\sqrt{3}}{\sqrt{4-3}}=-2\sqrt{3}\)
\(A=\dfrac{\sqrt{2}\left(1+\sqrt{5}\right)}{2+\sqrt{6+2\sqrt{5}}}+\dfrac{\sqrt{2}\left(1-\sqrt{5}\right)}{2-\sqrt{6-2\sqrt{5}}}\)
\(=\dfrac{\sqrt{2}\left(1+\sqrt{5}\right)}{2+\sqrt{\left(\sqrt{5}+1\right)^2}}+\dfrac{\sqrt{2}\left(1-\sqrt{5}\right)}{2-\sqrt{\left(\sqrt{5}-1\right)^2}}\)
\(=\dfrac{\sqrt{2}\left(1+\sqrt{5}\right)}{2+\sqrt{5}+1}+\dfrac{\sqrt{2}\left(1-\sqrt{5}\right)}{2-\left(\sqrt{5}-1\right)}\)
\(=\dfrac{\sqrt{2}\left(1+\sqrt{5}\right)}{3+\sqrt{5}}+\dfrac{\sqrt{2}\left(1-\sqrt{5}\right)}{3-\sqrt{5}}\)
\(=\sqrt{2}\left(\dfrac{\left(1+\sqrt{5}\right)\left(3-\sqrt{5}\right)+\left(1-\sqrt{5}\right)\left(3+\sqrt{5}\right)}{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}\right)\)
\(=\sqrt{2}.\left(\dfrac{-4}{9-5}\right)=-\sqrt{2}\)

A = (\(x+y\))2 - 2.(\(x+y\))z + 4z2
A = (\(x+y\))2 - 2.(\(x+y\))z + (2z)2
A = (\(x+y\) - 2z)2
A = (\(x+y\) - 2z)(\(x+y\) - 2z)

Họ đã bán số cam là:
1000.\(\dfrac{5}{8}\)= 625 (quả)
Còn lại số cam là:
1000- 625= 375 ( quả)
Vậy cửa hàng còn 375 quả

Gọi số phải tìm là: A
A:72=C dư 49 => A=Cx72+49 A:75=C dư 28 => A=Cx75+28
Vậy ta có Cx72+49=Cx75+28
75xC-72xC=49-28
3xC = 21
C = 21:3=7
=> =72x7+49 =553
Vậy số cần tìm là : 553

\(D=\dfrac{2^2-1}{2^2}+\dfrac{3^2-1}{3^2}+...+\dfrac{2025^2-1}{2025^2}\)
\(=\left(\dfrac{2^2}{2^2}+\dfrac{3^2}{3^2}+...+\dfrac{2025^2}{2025^2}\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2025^2}\right)\)
\(=\left(1+1+...+1\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2025^2}\right)\)
\(=2024-\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+....+\dfrac{1}{2025^2}\right)\)
Đặt \(E=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2025^2}\)
Do \(E>0\Rightarrow D< 2024\) (1)
Lại có:
\(E< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2024.2025}\)
\(E< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2024}-\dfrac{1}{2025}\)
\(E< 1-\dfrac{1}{2025}< 1\)
\(\Rightarrow D-E>2024-1=2023\) (2)
(1);(2) \(\Rightarrow2023< D< 2024\)
\(\Rightarrow D\) nằm giữa 2 số tự nhiên liên tiếp nên D ko thể là số tự nhiên
A tích của hai số là 276 nếu thêm vào số thứ nhất 19 đơn vị thì tích của hai số là 713 tìm hai số đó

Gọi hai thừa số lần lượt là a;b.
a.b=276
(a+19).b=713
a.b+b.19=713
b.19=713-276
b.19=437
b=437:19
b=23
a=276:23
a=12
Vậy hai số đó là 12 và 23

\(\Leftrightarrow x^2+2y^2+3xy-4x-5y+3=4\)
\(\Leftrightarrow\left(x^2+2xy-3x\right)+\left(xy+2y^2-3y\right)-\left(x+2y-3\right)=4\)
\(\Leftrightarrow x\left(x+2y-3\right)+y\left(x+2y-3\right)-\left(x+2y-3\right)=4\)
\(\Leftrightarrow\left(x+2y-3\right)\left(x+y-1\right)=4\)
Ta có bảng:
| x+2y-3 | -4 | -2 | -1 | 1 | 2 | 4 |
| x+y-1 | -1 | -2 | -4 | 4 | 2 | 1 |
| x | 1 | -3 | -8 | 6 | 1 | -3 |
| y | -1 | 2 | 5 | -1 | 2 | 5 |
Vậy \(\left(x;y\right)=\left(1;-1\right);\left(-3;2\right);\left(-8;5\right);\left(6;-1\right);\left(1;2\right);\left(-3;5\right)\)

Bạn xem lại đề, quy luật của các số hạng trong tổng có vẻ chưa rõ ràng lắm.
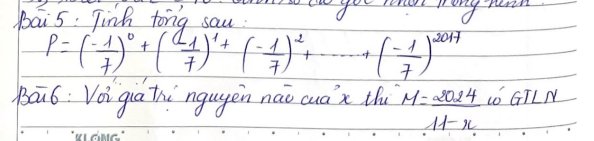
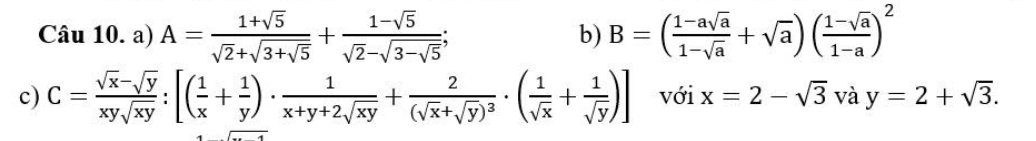

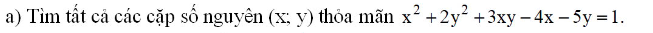
3,2>3,1>2,8
vì 2,8 < 3,11 < 3,2 Vậy số lớn nhất là số 3,2