Viết đoạn văn ngắn miêu tả về mùa xuân có xử dụng biện pháp tu từ so sánh và nhân hoá
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a; (\(\dfrac{1}{x}\) - 5)(\(\dfrac{1}{x}\) + 5)
= (\(\dfrac{1}{x}\))2 - 52
= \(\dfrac{1}{x^2}\) - 25
b; (\(\dfrac{x}{3}\) - \(\dfrac{y}{4}\))(\(\dfrac{x}{3}\) + \(\dfrac{y}{4}\))
= \(\left(\dfrac{x}{3}\right)^2\) - \(\left(\dfrac{y}{4}\right)^2\)
= \(\dfrac{x^2}{9}\) - \(\dfrac{y^2}{16}\)
d; (\(\dfrac{x}{y}\) - \(\dfrac{2}{3}\) (\(\dfrac{x}{y}\)+\(\dfrac{2}{3}\))
= (\(\dfrac{x}{y}\))2 - (\(\dfrac{2}{3}\))2
= \(\dfrac{x^2}{y^2}\) - \(\dfrac{4}{9}\)
e; (2\(x\) - \(\dfrac{2}{3}\))(\(\dfrac{2}{3}\) + 2\(x\))
= (2\(x\))2 - (\(\dfrac{2}{3}\))2
= 4\(x^2\) - \(\dfrac{4}{9}\)

Đổi:\(\dfrac{39}{6}=\dfrac{13}{2}\)
Chiều rộng mảnh đất là:
\(\dfrac{13}{2}\times\dfrac{1}{3}=\dfrac{13}{6}\left(cm\right)\)
Chu vi mảnh đất là:
\(2\times\left(\dfrac{13}{6}+\dfrac{13}{2}\right)=\dfrac{52}{3}\left(m\right)\)
Diện tích mảnh đất là:
\(\dfrac{13}{6}\times\dfrac{13}{2}=\dfrac{169}{12}\left(m^2\right)\)
Đ/S:...

\(S=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{200}}\)
\(\Rightarrow2S=2\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{200}}\right)\)
\(\Rightarrow2S=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{199}}\)
\(\Rightarrow2S-S=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{199}}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{200}}\right)\)
\(\Rightarrow S=1-\dfrac{1}{2^{100}}< 1\)
\(\Rightarrow S< 1\)
Vậy \(S< 1\)

\(1.2\left(x+2\right)^2< 2x\left(x+2\right)+4\\ \Leftrightarrow2\left(x^2+4x+4\right)-2x\left(x+2\right)-4< 0\\ \Leftrightarrow2x^2+8x+4-2x^2-4x-4< 0\\ \Leftrightarrow4x< 0\\ \Leftrightarrow x< 0\\ 2.\left(x-1\right)^2+x^2< \left(x+1\right)^2+\left(x+2\right)^2\\ \Leftrightarrow x^2-2x+1+x^2< x^2+2x+1+x^2+4x+4\\ \Leftrightarrow2x^2-2x+1-2x^2-6x-5< 0\\ \Leftrightarrow-8x-4< 0\\ \Leftrightarrow8x>-4\\ \Leftrightarrow x>-\dfrac{1}{2}\\ 3.\left(x^2+1\right)\left(x-6\right)< \left(x-2\right)^3\\ \Leftrightarrow x^3-6x^2+x-6< x^3-6x^2+12x-8\\ \Leftrightarrow x-6< 12x-8\\ \Leftrightarrow12x-x>-6+8\\ \Leftrightarrow11x>2\\ \Leftrightarrow x>\dfrac{2}{11}\)

a: Xét ΔBAD và ΔABC có
AB chung
BD=AC
AD=BC
Do đó: ΔBAD=ΔABC
=>\(\widehat{ABD}=\widehat{BAC}\)
=>\(\widehat{TAB}=\widehat{TBA}\)
=>ΔTAB cân tại T
=>TA=TB
b: Ta có: TA+TC=AC
TB+TD=BD
mà TA=TB và AC=BD
nên TC=TD
nối t với m sao cho tm vuông góc ab
xét tam giác AMT và tam giác BMT có
amt=bmt=90 độ
mt chung
am=mb
suy ra hai tam giác bằng nhau
suy ra ta=tb
CMTT ta có tam giác TDN và TCN
suy ra TD=TC

Bài 18:
a: \(\left(-\dfrac{40}{51}\cdot0,32\cdot\dfrac{17}{20}\right):\dfrac{64}{75}\)
\(=-\dfrac{40}{20}\cdot\dfrac{17}{51}\cdot\dfrac{8}{25}\cdot\dfrac{75}{64}\)
\(=-\dfrac{2}{3}\cdot\dfrac{8}{64}\cdot\dfrac{75}{25}=-\dfrac{2}{3}\cdot3\cdot\dfrac{1}{8}=-\dfrac{2}{8}=-\dfrac{1}{4}\)
b: \(-\dfrac{10}{11}\cdot\dfrac{8}{9}+\dfrac{7}{18}\cdot\dfrac{10}{11}=\dfrac{10}{11}\left(-\dfrac{8}{9}+\dfrac{7}{18}\right)\)
\(=\dfrac{10}{11}\left(-\dfrac{16}{18}+\dfrac{7}{18}\right)=\dfrac{10}{11}\cdot\dfrac{-9}{18}=\dfrac{10}{11}\cdot\dfrac{-1}{2}=-\dfrac{5}{11}\)
c: \(\dfrac{3}{14}:\dfrac{1}{28}-\dfrac{13}{21}:\dfrac{1}{28}+\dfrac{29}{42}:\dfrac{1}{28}-8\)
\(=\left(\dfrac{3}{14}-\dfrac{13}{21}+\dfrac{29}{42}\right):\dfrac{1}{28}-8\)
\(=\left(\dfrac{9}{42}-\dfrac{6}{42}+\dfrac{29}{42}\right):\dfrac{1}{28}-8\)
\(=\dfrac{32}{42}\cdot28-8=32\cdot\dfrac{2}{3}-8=\dfrac{64}{3}-\dfrac{24}{3}=\dfrac{40}{3}\)
d: \(-1\dfrac{5}{7}\cdot15+\dfrac{2}{7}\cdot\left(-15\right)+\left(-105\right)\left(\dfrac{2}{3}-\dfrac{4}{5}+\dfrac{1}{7}\right)\)
\(=-\dfrac{12}{7}\cdot15+\dfrac{2}{7}\cdot\left(-15\right)+\left(-105\right)\left(\dfrac{70}{105}-\dfrac{84}{105}+\dfrac{15}{105}\right)\)
\(=\dfrac{-180-30}{7}+\left(-105\right)\cdot\dfrac{1}{105}\)
=-30-1=-31
Bài 19:
a: \(A=7x-2x-\dfrac{2}{3}y+\dfrac{7}{9}y=5x+y\left(\dfrac{7}{9}-\dfrac{2}{3}\right)=5x+\dfrac{y}{9}\)
Khi x=-1/10;y=4,8 thì \(A=5\cdot\dfrac{-1}{10}+\dfrac{4.8}{9}\)
\(=-\dfrac{1}{2}+\dfrac{8}{15}=\dfrac{-15+16}{30}=\dfrac{1}{30}\)
b: \(B=x+\dfrac{0,2-0,375+\dfrac{5}{11}}{-0,3+\dfrac{9}{16}-\dfrac{15}{22}}\)
\(=x+\dfrac{\dfrac{2}{10}-\dfrac{6}{16}+\dfrac{10}{22}}{-\dfrac{3}{10}+\dfrac{9}{16}-\dfrac{15}{22}}=x+\dfrac{2\left(\dfrac{1}{10}-\dfrac{3}{16}+\dfrac{5}{22}\right)}{-3\left(\dfrac{1}{10}-\dfrac{3}{16}+\dfrac{5}{22}\right)}\)
\(=x-\dfrac{2}{3}\)
Khi x=-1/3 thì \(B=-\dfrac{1}{3}-\dfrac{2}{3}=-\dfrac{3}{3}=-1\)

Giá tiền mỗi buổi học trực tuyến là \(150000\times\dfrac{8}{15}=80000\left(đồng\right)\)
Số buổi học trong 1 năm là 4x12=48(buổi)
Số tiền tiết kiệm được là:
\(48\times\left(150000-80000\right)=48\times70000=3360000\left(đồng\right)\)

Hướng giải:
- Chứng minh được đường phân giác trong và đường phân giác ngoài của cùng 1 góc thì vuông góc với nhau
- Từ đó chững minh được APBQ và AMCN là hình chữ nhật.
- Gọi I là giao của PQ với AB; K là giao của MN với AC => I là trung điểm của AB và K là trung điểm của AC (trong HCN 2 đường chéo cắt nhau tại trung điểm mỗi đường)
- Ta chứng minh được \(\widehat{QNy}=\widehat{BCy}\) Hai góc này ở vị trí đồng vị
=> MN//BC
- Chứng minh tương tự ta cũng có PQ//BC
- Xét tg ABC có PQ đi qua trung điểm AB và PQ//BC => PQ đi qua trung điểm K của AC (Trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
=> Qua điểm K có 2 đường thẳng PQ và MN cùng song song với BC nên MN trùng PQ hay P; Q; M; N thẳng hàng (Từ 1 điểm bên ngoài 1 đường thẳng cho trước chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho)
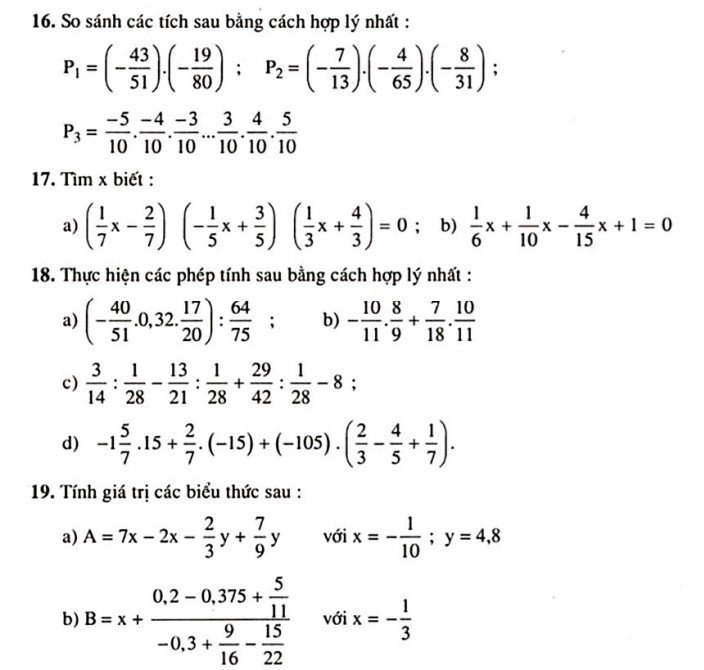
Sau chuỗi ngày đông lạnh giá, thành phố Hà Nội thân yêu của chúng tôi bước sang những ngày xuân ấm áp vui tươi. Từ trên cao nhìn xuống, nơi đây tựa như một bức tranh tuyệt đẹp do một nghệ sĩ nào đó của đất trời tạo nên. Bầu trời Hà Nội mùa xuân dường như mang một vẻ gì đó khó tả. Nó khoác lên mình chiếc áo xanh dịu dàng, khác hẳn chiếc áo xám xịt của mùa đông. Với một bầu không khí thoáng đãng đặc biệt, con người ta chẳng thể không cảm thấy dễ chịu xen chút ngỡ ngàng trước những lần đổi thay ấn tượng của tạo hóa. Nhắc đến những ngày xuân của Hà Nội, sao không thể thiếu những cơn mưa xuân lớt phớt, nhẹ nhàng như nàng thiếu nữ rắc xuống nhân gian các hạt mưa bay bay, làm cây cối bừng tỉnh sau giấc ngủ dài lạnh lẽo của mùa đông vừa qua. Trong không gian thoang thoảng những hương thơm dìu dịu của hoa đào, hoa mai thêm chút của chàng quất kia, dòng người cứ tấp nập qua lại, người sắm áo quần, người nhộn nhịp bệ những chậu đào, cành mai, cây quất,... Ôi mùa xuân, mùa của muôn loài!
(Mình ko chép mạng nha, bạn cho mình một tick có được ko ạ? ^^)