so sánh A= -7/10^2023 +-15/10^2024 B=-15/10^2023+-7/10^2024
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) -2/5 + 1/(-4) - 4/3
= -2/5 - 1/4 - 4/3
= -13/20 - 4/3
= -119/60
b) -8/5 . 19/29 + 8/(-5) . 3/29 - 7/29 . 8/5
= -8/5 . (19/29 + 3/29 + 7/29)
= -8/5 . 1
= -8/5
c) 1,25 . [(15% - 1 1/3) - 4/5 . 1,8]
= 5/4 . [(3/20 - 4/3) - 9/2 . 9/5]
= 5/4 . (-71/60 - 81/10)
= 5/4 . (-557/60)
= -557/48

15 quả táo cuối cùng chiếm:
\(1-\dfrac{1}{4}=\dfrac{3}{4}\)(số quả táo còn lại sau lần 2)
Số quả táo còn lại sau lần 2 là:
\(15:\dfrac{3}{4}=15\times\dfrac{4}{3}=20\left(quả\right)\)
2/3 số táo còn lại sau lần 1 là:
20+10=30(quả)
Số táo còn lại sau lần 1 là:
\(30:\dfrac{2}{3}=30\times\dfrac{3}{2}=45\left(quả\right)\)
1/2 số táo ban đầu là 45+5=50(quả)
Số táo ban đầu là \(50:\dfrac{1}{2}=100\left(quả\right)\)
Để giải bài toán này theo cách giải của học sinh lớp 6, chúng ta sẽ thực hiện từng bước một: Bước 1: Gọi số lượng táo ban đầu mà bác An mang đi bán là \(x\). Bước 2: Người thứ nhất mua \(\frac{1}{2}\) số táo và thêm 5 quả, tức là \(\frac{1}{2}x + 5\) quả. Bước 3: Số táo còn lại sau khi người thứ nhất mua là \(x - (\frac{1}{2}x + 5) = \frac{1}{2}x - 5\) quả. Bước 4: Người thứ hai mua \(\frac{1}{3}\) số táo còn lại và thêm 10 quả, tức là \(\frac{1}{3}(\frac{1}{2}x - 5) + 10\) quả. Bước 5: Số táo còn lại sau khi người thứ hai mua là \(\frac{1}{2}x - 5 - \frac{1}{3}(\frac{1}{2}x - 5) - 10 = \frac{1}{6}x - \frac{5}{3}\) quả. Bước 6: Người thứ ba mua \(\frac{1}{4}\) số táo còn lại lúc đó, tức là \(\frac{1}{4}(\frac{1}{6}x - \frac{5}{3})\) quả. Bước 7: Số táo còn lại sau khi người thứ ba mua là \(\frac{1}{6}x - \frac{5}{3} - \frac{1}{4}(\frac{1}{6}x - \frac{5}{3}) = \frac{1}{12}x - \frac{5}{4}\) quả. Bước 8: Người thứ tư mua 15 quả nữa thì hết số táo bác An đưa đi bán, tức là \(\frac{1}{12}x - \frac{5}{4} - 15 = 0\). Bước 9: Giải phương trình \(\frac{1}{12}x - \frac{5}{4} - 15 = 0\) để tìm ra giá trị của \(x\), sau đó tính số bao táo bác An đã mang đi bán. Hy vọng cách giải này giúp bạn hiểu và giải quyết bài toán. Nếu cần hỗ trợ thêm, đừng ngần ngại để lại câu hỏi.

\(\dfrac{x}{3}-\dfrac{2}{y}=\dfrac{1}{5}\)
=>\(\dfrac{xy-6}{3y}=\dfrac{1}{5}\)
=>5(xy-6)=3y
=>5xy-3y=30
=>y(5x-3)=30
=>(5x-3;y)\(\in\){(1;30);(30;1);(-1;-30);(-30;-1);(2;15);(15;2);(-2;-15);(-15;-2);(3;10);(10;3);(-3;-10);(-10;-3);(5;6);(6;5);(-5;-6);(-6;-5)}
=>(x;y)\(\in\){(4/5;30);(33/5;1);(2/5;-30);(-27/5;-1);(1;15);(18/5;2);(1/5;-15);(-12/5;-2);(6/5;10);(13/5;3);(0;-10);(-7/5;-3);(8/5;6);(9/5;5);(-2/5;-6);(-3/5;-5)}

Giải:
\(\dfrac{12}{4}\) = \(3\)
\(\dfrac{4}{12}\) = \(\dfrac{1}{3}\)
#hoctot!
mình cx k hiểu ý bạn lắm nên mk làm đại ạ:))

Ngày thứ hai đọc được:
\(\dfrac{1}{6}\cdot2=\dfrac{1}{3}\)(cuốn sách)
Sau hai ngày thì số phần sách còn lại chưa đọc là:
\(1-\dfrac{1}{3}-\dfrac{1}{6}=\dfrac{1}{2}\)
30 trang cuối cùng chiếm:
\(\dfrac{1}{2}\left(1-\dfrac{2}{3}\right)=\dfrac{1}{2}\cdot\dfrac{1}{3}=\dfrac{1}{6}\)(cuốn sách)
Số trang của cuốn sách là \(30:\dfrac{1}{6}=30\cdot6=180\left(trang\right)\)

Vd: Năng lượng từ ánh sáng mặt trời đến pin mặt trời (Quang năng ---> Hóa năng)

\(\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+...+\dfrac{1}{\dfrac{x\left(x+1\right)}{2}}=\dfrac{2019}{2021}\)
=>\(\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{20}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{2019}{2021}\)
=>\(2\left(\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{x\left(x+1\right)}\right)=\dfrac{2019}{2021}\)
=>\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{2019}{4042}\)
=>\(\dfrac{1}{2}-\dfrac{1}{x+1}=\dfrac{2019}{4042}\)
=>\(\dfrac{1}{x+1}=\dfrac{1}{2}-\dfrac{2019}{4042}=\dfrac{2021-2019}{4042}=\dfrac{2}{4042}=\dfrac{1}{2021}\)
=>x+1=2021
=>x=2020
\(\Leftrightarrow\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{20}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{2019}{2021}\)
\(\Leftrightarrow\dfrac{2}{2.3}+\dfrac{2}{3.4}+\dfrac{2}{4.5}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{2019}{2021}\)
\(\Leftrightarrow2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{x}-\dfrac{1}{x+1}\right)=\dfrac{2019}{2021}\)
\(\Leftrightarrow2\left(\dfrac{1}{2}-\dfrac{1}{x+1}\right)=\dfrac{2019}{2021}\)
\(\Leftrightarrow1-\dfrac{2}{x+1}=\dfrac{2019}{2021}\)
\(\Leftrightarrow\dfrac{2}{x+1}=1-\dfrac{2019}{2021}\)
\(\Leftrightarrow\dfrac{2}{x+1}=\dfrac{2}{2021}\)
\(\Rightarrow x+1=2021\)
\(\Rightarrow x=2020\)

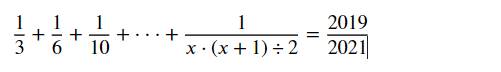

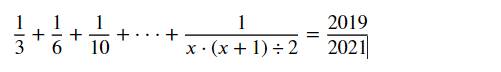
A = -7/10²⁰²³ + (-15/10²⁰²⁴)
= (-70 - 15)/10²⁰²⁴
= -85/10²⁰²⁴
B = -15/10²⁰²³ + (-7/10²⁰²⁴)
= (-150 - 7)/10²⁰²⁴
= -157/10²⁰²⁴
Do -85 > -157 nên -85/10²⁰²⁴ > -157/10²⁰²⁴
Vậy A > B