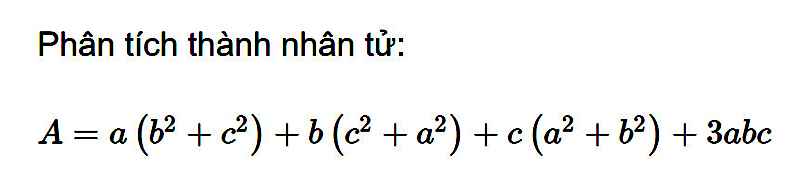
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do khi chia x cho 2; 3; 4; 5; 6 đều dư 1 nên x - 1 chia hết cho 2; 3; 4; 5; 6
x - 1 BC(2; 3; 4; 5; 6)
Ta có:
2 = 2
3 = 3
4 = 2²
5 = 5
6 = 2.3
⇒ BCNN(2; 3; 4; 5; 6) = 2².3.5 = 60
⇒ x - 1 ∈ BC(2; 3; 4; 5; 6) = B(60) = {0; 60; 120; 180; 240; 300; ...}
⇒ x ∈ {1; 61; 121; 181; 241; 301; ...}
Mà 301 ⋮ 7
⇒ x = 301

Đặt \(P\left(x\right)=x^3+3x^2-x+3^n\)
Nếu \(P\left(x\right)\) có nghiệm hữu tỉ \(x=\dfrac{p}{q}\left(p\inℤ,q\inℕ^∗;\left(p,q\right)=1\right)\) thì \(p|3^n,q|1\Rightarrow q=1\) và \(p=3^k\left(k\le n\right)\)
Vậy \(x=3^k\) sẽ là nghiệm hữu tỉ duy nhất của \(P\left(x\right)\) hay \(P\left(3^k\right)=0\)
\(\Leftrightarrow\left(3^k\right)^3+3.\left(3^k\right)^2-3^k+3^n=0\)
\(\Leftrightarrow3^{3k}+3^{2k+1}-3^k+3^n=0\)
\(\Leftrightarrow3^{2k}+3^{k+1}-1+3^{n-k}=0\)
Ta thấy với \(n>k\) thì \(3^{2k}+3^{k+1}+3^{n-k}⋮3\) và \(0⋮3\) nên từ đây suy ra \(1⋮3\), vô lý.
Với \(n=k\) thì \(3^{2n}+3^{n+1}=0\), vô lý vì \(3^{2n}+3^{n+1}>0\) với \(n\inℕ^∗\)
Vậy \(P\left(x\right)\) không thể có nghiệm hữu tỉ. Do đó, nếu \(x^3+3x^2-x+3=0\) thì \(x\) chỉ có thể là một số vô tỉ. (đpcm)

Số học sinh giỏi của lớp:
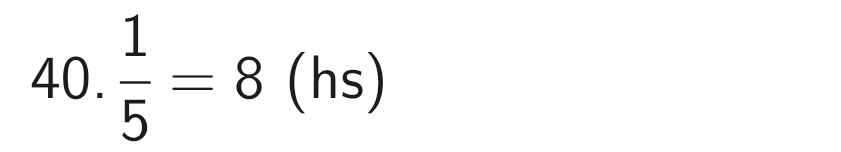 Số học sinh khá của lớp:
Số học sinh khá của lớp:
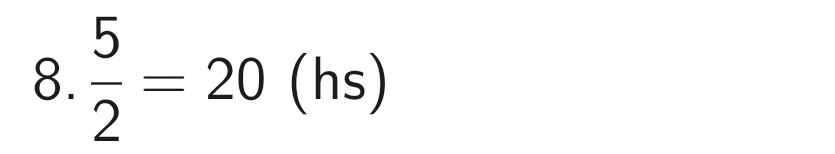 Số học sinh trung bình của lớp:
Số học sinh trung bình của lớp:
20 . 50% = 10 (hs)
Số học sinh yếu của lớp:
40 - 8 - 20 - 10 = 2 (hs)
b) Tỉ số phần trăm học sinh yếu so với cả lớp:
2 . 100% : 40 = 5%

1 + 34 - 12 - 3 + 2
= 35 - 12 - 3 + 2
= 23 - 3 + 2
= 20 + 2
= 22

1 năm nhuận có bao nhiêu ngày? = > 366 ngày. (Kiến thức bổ sung : 4 năm mới có 1 năm nhuận)
1 năm thường có bao nhiêu ngày? = > 365 ngày.
1 thế kỉ có bao nhiêu năm? = > 100 năm.
1 giờ có bao nhiêu phút? = > 60 phút.
1 phút có bao nhiêu giây? = > 60 giây.
1 giây có bao nhiêu tíc- tắc? = > 60 tích tắc.
1 ngày có bao nhiêu giờ? = > 24 giờ.
1 tuần có bao nhiêu ngày? => 7 ngày.
366 ngày.
= > 365 ngày.
= > 100 năm.
= > 60 phút.
= > 60 giây.
= > 60 tích tắc.
= > 24 giờ.
=> 7 ngày.



A = a(b² + c²) + b(a² + c²) + c(a² + b²) + 3abc
= ab² + ac² + a²b + bc² + a²c + b²c + 3abc
= (ab² + a²b + abc) + (a²c + ac² + abc) + (b²c + bc² + abc)
= ab(a + b + c) + ac(a + c + b) + bc(b + c + a)
= (a + b + c)(ab + ac + bc)