1. Nêu các nhóm chất dinh dưỡng? Nhóm nào được khuyến cáo dùng ít trong khẩu phần?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có
\(\dfrac{BM}{AM}=\dfrac{BC}{AC}=\dfrac{a}{b}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
\(\dfrac{CN}{AN}=\dfrac{BC}{AB}=\dfrac{a}{b}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
\(\Rightarrow\dfrac{BM}{AM}=\dfrac{CN}{AN}\Rightarrow\dfrac{BM}{CN}=\dfrac{AM}{AN}\) => MN//BC (Talet)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MN}{BC}\Rightarrow\dfrac{AM}{b}=\dfrac{MN}{a}\) (1)
Ta có
\(\dfrac{AM}{BM}=\dfrac{AC}{BC}=\dfrac{b}{a}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
\(\Rightarrow\dfrac{AM}{b}=\dfrac{BM}{a}=\dfrac{AM+BM}{a+b}=\dfrac{AB}{a+b}=\dfrac{b}{a+b}\)
\(\Rightarrow AM=\dfrac{b^2}{a+b}\) Thay vào (1)
\(\Rightarrow\dfrac{\dfrac{b^2}{a+b}}{b}=\dfrac{MN}{a}\Rightarrow\dfrac{b}{a+b}=\dfrac{MN}{a}\Rightarrow MN=\dfrac{ab}{a+b}\)
Ta có
(Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
(Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
=> MN//BC (Talet)
(1)
Ta có
(Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
Thay vào (1)


3x² + 2x - 1
= 3x² + 3x - x - 1
= (3x² + 3x) - (x + 1)
= 3x(x + 1) - (x + 1)
= (x + 1)(3x - 1)

\(\left(-\dfrac{3x}{5y^2}\right).\left(-\dfrac{5y^2}{6x^3}\right)\)
\(=\dfrac{-3x.\left(-5y^2\right)}{5y^2.6x^3}\)
\(=\dfrac{1}{2x^2}\)

Hiện tượng sử dụng chất gây nghiện trong học đường ngày nay là một vấn đề đáng lo ngại và cần được quan tâm. Đây là một hiện tượng có thể gây hại nghiêm trọng cho sức khỏe và sự phát triển của các em học sinh.
Sự sử dụng chất gây nghiện trong học đường có thể xuất phát từ nhiều nguyên nhân, bao gồm áp lực học tập, cảm giác căng thẳng, muốn tăng cường khả năng tập trung và năng suất làm việc. Tuy nhiên, việc sử dụng chất gây nghiện không chỉ không giải quyết được vấn đề này mà còn tạo ra những hệ quả tiêu cực.
Việc sử dụng chất gây nghiện có thể ảnh hưởng đến sức khỏe tâm lý và thể chất của học sinh. Chất gây nghiện có thể gây ra các vấn đề như mất ngủ, lo âu, trầm cảm, suy giảm khả năng tư duy và học tập. Ngoài ra, sử dụng chất gây nghiện cũng có thể gây ra các vấn đề về hành vi, như xâm phạm quyền riêng tư, vi phạm luật pháp và gây rối trật tự trong học đường.
Để giải quyết vấn đề này, cần có sự tham gia và hỗ trợ từ các bên liên quan, bao gồm gia đình, trường học và cộng đồng. Các biện pháp như tăng cường giáo dục về tác hại của chất gây nghiện, xây dựng môi trường học tập lành mạnh và hỗ trợ tâm lý cho học sinh có thể giúp ngăn chặn và giảm thiểu hiện tượng này.
Ngoài ra, cần tạo ra một môi trường học tập thoải mái và không gây áp lực quá lớn cho học sinh. Đồng thời, cần khuyến khích học sinh tham gia vào các hoạt động ngoại khóa và thể dục để giảm căng thẳng và tăng cường sức khỏe tâm lý.
Tóm lại, hiện tượng sử dụng chất gây nghiện trong học đường ngày nay là một vấn đề nghiêm trọng. Để giải quyết vấn đề này, cần có sự tham gia và hỗ trợ từ các bên liên quan và tạo ra một môi trường học tập lành mạnh và thoải mái cho học sinh.

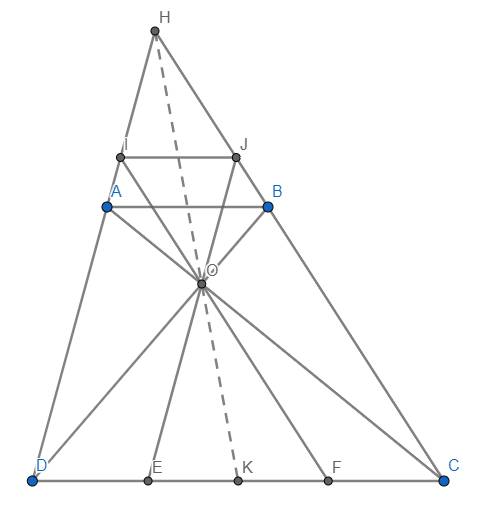
b) Theo Thales: \(\dfrac{DE}{DC}=\dfrac{AO}{AC};\dfrac{CF}{CD}=\dfrac{BO}{BD}\)
Theo câu a thì \(\dfrac{AO}{AC}=\dfrac{BO}{BD}\) \(\Rightarrow\dfrac{DE}{DC}=\dfrac{CF}{CD}\Rightarrow DE=CF\) (đpcm)
c) Từ \(DE=CF\Rightarrow\dfrac{DE}{EF}=\dfrac{CF}{EF}\)
Mà theo Thales: \(\dfrac{DE}{EF}=\dfrac{IO}{OF};\dfrac{CF}{EF}=\dfrac{JO}{OE}\)
Do đó \(\dfrac{IO}{OF}=\dfrac{JO}{OE}\) \(\Rightarrow\) IJ//CD//AB
d) Dùng định lý Menelaus đảo nhé bạn. Ta có \(\dfrac{HA}{HD}=\dfrac{AB}{CD}=\dfrac{OA}{OC}\) nê \(\dfrac{HA}{AD}.\dfrac{OC}{OA}=1\). Do K là trung điểm EF mà \(DE=CF\) nên K cũng là trung điểm CD hay \(\dfrac{KD}{KC}=1\). Do đó \(\dfrac{HA}{AD}.\dfrac{KD}{KC}.\dfrac{OC}{OA}=1\). Theo định lý Menalaus đảo \(\Rightarrow\)H, O, K thẳng hàng (đpcm)
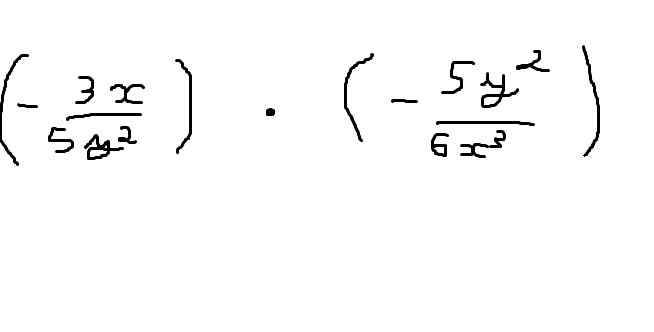
Bạn xem trong sách nhé, có đó.
tui ko bt(0-o)