a; A = (3².5 - 160: 2²) + 2024

   A = (9.5 - 160 : 4) + 2024

  A = (45 - 40) + 2024

  A = 5 + 2024

  A = 2029

b; B = (-360) - (-87) + 69 - 87

    B = -360 + 87 + 69 - 87

    B = - (360 - 69) + (87 - 87)

    B = - 291 + 0

    B = -291

c; C = 182.26 - 82.26 + 500

   C  = 26.(182 - 82) + 500

   C  = 26.100 + 500

   C   = 2600 + 500

  C   = 3100 

Tổng của ô thứ ba, ô thứ tư và ô thứ năm là:

         100 - 17  = 83

Số ở ô thứ sáu là:

       100 - 83 = 17

Số ở ô thứ năm là:

        100 - (36 + 17 + 19) = 28

Số ở ô thứ ba là:

     100 - (36 + 28 + 17)  = 19

Số ở ô thứ nhất là:

      100 - (17 + 19 + 36) = 28

Số ở ô thứ tám là: 

      100 - (19 + 17 + 28) = 36

Số ở ô thứ chín là: 

         100 - ( 36 + 19 + 17) = 28

Số ở ô thứ mười là:

   100 - (28 + 36 + 19) = 17

Ta có bảng sau:

A là khẳng định đúng, \(5\in M\)

A. 5∈M

Vì chuyển dấu phẩy của số đó sang bên phải một hàng ta được số A nên số A bằng 10 lần số đã cho.

Vì dời dấu phẩy của số đó sang trái một hàng ta được số B nên số B bằng:     \(\dfrac{1}{10}\) số đã cho

Tỉ  số của số B và số A là:

      \(\dfrac{1}{10}\) : 10 = \(\dfrac{1}{100}\)

Ta có sơ đồ:

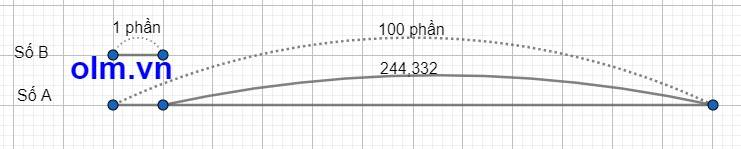
Theo sơ đồ ta có: 

Số B là: 244,332 : (100 - 1) = 2,468

Số đã cho là : 2,468 x 10 = 24,68

Đáp số:... 

Vì chuyển dấu phẩy của số đó sang bên phải một hàng ta được số A nên số A bằng 10 lần số đã cho.

Vì dời dấu phẩy của số đó sang trái một hàng ta được số B nên số B bằng:     $\genfrac{}{}{0ex}{}{1}{10}$ số đã cho

Tỉ  số của số B và số A là:

      $\genfrac{}{}{0ex}{}{1}{10}$ : 10 = $\genfrac{}{}{0ex}{}{1}{100}$
 

Số B là: 244,332 : (100 - 1) = 2,468

Số đã cho là : 2,468 x 10 = 24,68

Bài 10

a; Giao của d1 với trục ox là điểm có hoành độ thỏa mãn

     \(x\) - 3 = 0 ⇒ \(x\) = 3

Giao của d1 với trục oy là điểm có tung độ thỏa mãn y = 0 - 3 = -3

Giao của d2 với trục ox là điểm có hoành độ thỏa mãn 

     3 - \(x\) = 0 ⇒ \(x\) = 3

Giao của d2 với trục oy là điểm có tung độ thỏa mãn y = 3 - 0 = 3

Ta có đồ thị d1 và d2 như hình dưới 

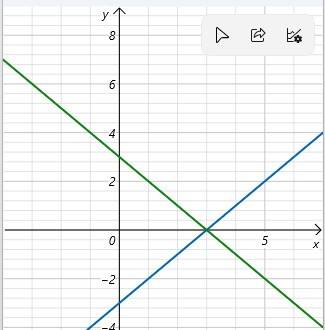
b; Giao của d1 và d2 là điểm có phương trình hoành độ thỏa mãn

\(x\) - 3 = 3 - \(x\)

2\(x\) = 6 

\(x\) = 6 : 2

\(x\) = 3; ⇒ y = 3- 3  =0 

Vậy giao của d1 và d2 là A(3;0)

Bài 9:

Giao của d1 với trục ox là điểm có hoành độ thỏa mãn 

              2\(x\) - 3  = 0 ⇒ \(x\) = \(\dfrac{3}{2}\)

Giao của d1 với trục oy là điểm có tung độ thỏa mãn

            y = 2.0 - 3  = - 3

Giao của d2 với trục ox là điểm có hoành độ thỏa mãn 

         -3 - \(x\) = 0 ⇒ \(x\) = 0

  Giao của d2 với trục oy là điểm có tung độ thỏa mãn

        y = -3 - 0 = -3

Ta có đồ thị như hình dưới đây

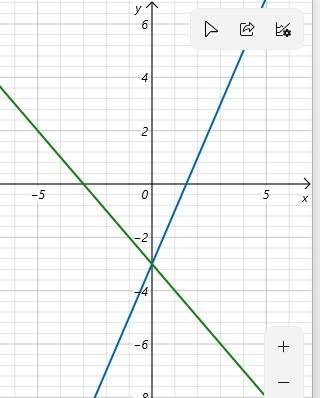
Giao của d1 và d2 là điểm có hoành độ thỏa mãn phương trình 

       2\(x\) - 3 = -3 - \(x\)

      2\(x\) + \(x\) = 0 

          3\(x\) =0 

            \(x\) = 0

    ⇒ y = -3 - 0 

       y = - 3

Vậy giao của d1 và d2 là điểm B(0; -3)

A = \(\dfrac{x+13}{x+2}\)  (đk \(x\) ≠ -2)

Em cần làm gì với biểu thức này?

Gọi ba cạnh của tam giác lần lượt là x,y,z (x,y,z >0)

Ta có ba cạnh của tam giác tỉ lệ với 2;4;5

\(\Rightarrow\dfrac{x}{2}=\dfrac{y}{4}=\dfrac{z}{5}\)

Áp dụng tính chất dãy tỉ số bằng nhau:

\(\dfrac{x}{2}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y+z}{2+4+5}=\dfrac{22}{11}=2\)

\(\Rightarrow\left\{{}\begin{matrix}x=2.2=4\left(cm\right)\\y=2.4=8\left(cm\right)\\z=2.5=10\left(cm\right)\end{matrix}\right.\)

Vậy ba cạnh của tam giác lần lượt là 4cm, 8cm và 10cm

Đặt \(A=7.5^{2n}+12.6^n=7.25^n+12.6^n\)

Do \(25\equiv6\left(mod19\right)\Rightarrow25^n\equiv6^n\left(mod19\right)\)

\(\Rightarrow A\equiv7.6^n+12.6^n\left(mod19\right)\)

\(\Rightarrow A\equiv19.6^n\left(mod19\right)\)

Do \(19.6^n⋮19\Rightarrow A⋮19\)

A = 7.5²ⁿ + 12.6ⁿ

A = 7.(5²)ⁿ + 12.6ⁿ

A = 7.25ⁿ + 12.6ⁿ

25  \(\equiv\) 6 (mod 19)

25ⁿ \(\equiv\) 6ⁿ (mod 19)

7    \(\equiv\) - 12 (mod 19)

⇒ 7.25ⁿ \(\equiv\) -12.6ⁿ (mod 19)

⇒ 7.25ⁿ -( -12.6ⁿ) ⋮ 19

⇒ 7.25ⁿ + 12.6ⁿ   ⋮ 19

a.

\(2^{2024}=2^2.2^{2022}=4.\left(2^3\right)^{674}=4.8^{674}\)

Do \(8\equiv1\left(mod7\right)\Rightarrow8^{674}\equiv1\left(mod7\right)\)

\(\Rightarrow4.8^{674}\equiv4\left(mod7\right)\)

Hay \(2^{2024}\) chia 7 dư 4

b.

\(5^{70}+7^{50}=\left(5^2\right)^{35}+\left(7^2\right)^{25}=25^{35}+49^{25}\)

Do \(\left\{{}\begin{matrix}25\equiv1\left(mod12\right)\\49\equiv1\left(mod12\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}25^{35}\equiv1\left(mod12\right)\\49^{25}\equiv1\left(mod12\right)\end{matrix}\right.\)

\(\Rightarrow25^{35}+49^{25}\equiv2\left(mod12\right)\)

Hay \(5^{70}+7^{50}\) chia 12 dư 2

c.

\(3^{2005}+4^{2005}=\left(3^5\right)^{401}+\left(4^5\right)^{401}=243^{401}+1024^{401}\)

Do \(\left\{{}\begin{matrix}243\equiv1\left(mod11\right)\\1024\equiv1\left(mod11\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}243^{401}\equiv1\left(mod11\right)\\1024^{401}\equiv1\left(mod11\right)\end{matrix}\right.\)

\(\Rightarrow243^{401}+1024^{401}\equiv2\left(mod11\right)\)

Hay \(3^{2005}+4^{2005}\) chia 11 dư 2

d.

\(1044\equiv1\left(mod7\right)\Rightarrow1044^{205}\equiv1\left(mod7\right)\)

Hay \(1044^{205}\) chia 7 dư 1

e.

\(3^{2003}=3^2.3^{2001}=9.\left(3^3\right)^{667}=9.27^{667}\)

Do \(27\equiv1\left(mod13\right)\Rightarrow27^{667}\equiv1\left(mod13\right)\)

\(\Rightarrow9.27^{667}\equiv9\left(mod13\right)\)

hay \(3^{2003}\) chia 13 dư 9

- \(\dfrac{5}{11}\) = \(\dfrac{20}{x}\) = \(\dfrac{-35}{y}\)

  \(x\)   = 20 : (-\(\dfrac{5}{11}\)) 

  \(x\) = -44

y = - 35 : (- \(\dfrac{5}{11}\))

y = 77