A  = n³ + 3n² + 2n

A = n(n² + 3n + 2)

A = n[(n² + n) + (2n + 2)]

A = n[n(n + 1) + 2(n + 1)]

A = n(n + 1)(n + 2)

+ Nếu n ⋮ 3 

⇒ A ⋮ 3; n và n + 1 là hai số tự nhiên liên tiếp nên sẽ có một số là số lẻ, một số là số chẵn nên n(n + 1) ⋮ 2 ⇒ A ⋮ 2

⇒ A \(\in\) B(2  ; 3); 2= 2; 3 = 3 ⇒ BCNN(2; 3) = 6 ⇒ A \(\in\) B(6) ⇒ A ⋮ 6

+ Nếu n không chia hết cho 3 thì n = 3k + 1 hoặc n = 3k + 2 ta có:

+ n = 3k + 1 thì n + 2 = 3k + 1 + 2 = 3k + ( 1 + 2) =  3k  +  3 ⋮ 3

+Nếu n = 3k  +  2 thì n + 1 = 3k + 2  + 1 = 3k + ( 2 + 1) = 3k +  3 ⋮ 3

Chứng minh tương tự với trường hợp A ⋮ 3 ở trên ta có A  là bội của 6 hay A ⋮ 6

Vậy A ⋮ 6 ∀ n \(\in\) Z⁺

a: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)

nên AMHN là hình chữ nhật

b: Xét ΔAHD có

AM là đường cao

AM là đường trung tuyến

Do đó: ΔAHD cân tại A

ΔAHD cân tại A

mà AB là đường cao

nên AB là phân giác của góc HAD

Xét ΔAHE có

AN là đường cao

AN là đường trung tuyến

Do đó: ΔAHE cân tại A

ΔAHE cân tại A

mà AC là đường cao

nên AC là phân giác của góc HAE

\(\widehat{DAE}=\widehat{DAH}+\widehat{EAH}\)

\(=2\cdot\left(\widehat{MAH}+\widehat{NAH}\right)\)

\(=2\cdot90^0=180^0\)

=>D,A,E thẳng hàng

           Giải:

\(\widehat{A}\)  - \(\widehat{D}\) = 30⁰ ⇒ \(\widehat{A}\) = 30⁰ + \(\widehat{D}\) 

Mặt khác \(\widehat{A}\) + \(\widehat{D}\) = 180⁰ (hai góc trong cùng phía)

           Thay A = 30⁰ + \(\widehat{D}\) vào \(\widehat{A}+\widehat{D}=180^0\) ta có:

\(30^0+\widehat{D}+\widehat{D}\) = 180⁰

          \(\widehat{D}+\widehat{D}\) = 180⁰ - 30⁰

              2\(\widehat{D}\)  = 150⁰

                \(\widehat{D}\)  = 150⁰ : 2 = 75⁰

\(\widehat{A}=30^0+75^0\) = 105⁰

\(\widehat{B}=5\widehat{C}\) ; \(\widehat{B}\) + \(\widehat{C}\) = 180⁰ (hai góc trong cùng phía)

5\(\widehat{C}\) + \(\widehat{C}\) = 180⁰ ⇒ 6\(\widehat{C}\) = 180⁰ ⇒ \(\widehat{C}=180^0:3\) = 60⁰

\(\widehat{B}\) = 180⁰ - 60⁰ = 150⁰

Đề thiếu rồi em, muốn tính được số đo các góc thì phải biết đâu là 2 đáy hình thang.

Ví dụ AB và CD là 2 đáy sẽ khác với AD và BC là 2 đáy

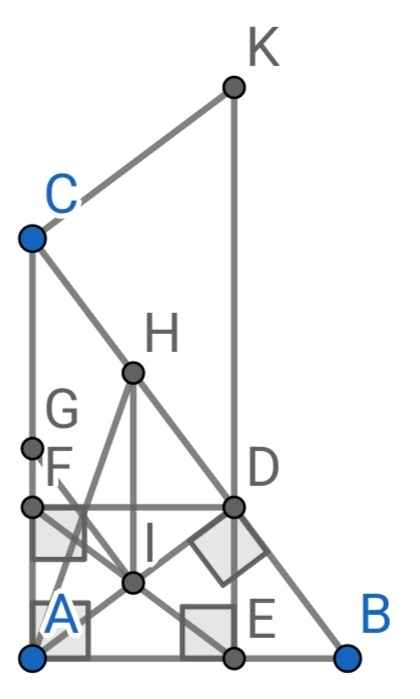
a) ∆ABC vuông tại A (gt)

⇒ AB ⊥ AC

⇒ ∠CAB = 90⁰

⇒ ∠EAF = 90⁰

Do E, F là hình chiếu của D lên AB, AC (gt)

⇒ ∠AED = ∠AFD = 90⁰

Tứ giác AEDF có:

∠EAF = ∠AED = ∠AFD = 90⁰ 

⇒ AEDF là hình chữ nhật

b) Do I là giao điểm của EF và AD (gt)

⇒ I là trung điểm của AD

Lại có:

H là trung điểm của DC (gt)

⇒ IH là đường trung bình của ∆ACD

⇒ IH // AC và IH = AC : 2

Do G là trung điểm của AC (gt)

⇒ CG = AC : 2

⇒ IH = CG = AC : 2

Do IH // AC (cmt)

⇒ IH // AG

Tứ giác IHCG có:

IH // CG (cmt)

IH = CG (cmt)

⇒ IHCG là hình bình hành

c) Do E là hình chiếu của D lên AB (gt)

⇒ DE ⊥ AB

Mà AC ⊥ AB (cmt)

⇒ DE // AC

⇒ DK // AC

Tứ giác ADKC có:

DK // AC (cmt)

DK = AC (gt)

⇒ ADKC là hình bình hành

⇒ CK // AD

d) Do IH // CG (cmt)

⇒ IH // AC

Mà AC ⊥ AB (cmt)

⇒ IH ⊥ AB

⇒ HI là đường cao của ∆HAB

Do AD là đường cao của ∆ABC (gt)

⇒ AD ⊥ BC

⇒ AD ⊥ BH

⇒ AD là đường cao của ∆HAB

∆HAB có:

HI là đường cao (cmt)

AD là đường cao thứ hai (cmt)

Mà I là giao điểm của HI và AD

⇒ I là giao điểm của ba đường cao của ∆HAB

⇒ I là trực tâm của ∆HAB

a: Xét tứ giác BHCK có

M là trung điểm chung của BC và HK

=>BHCK là hình bình hành

b: BHCK là hình bình hành

=>BH//CK và BK//CH

Ta có: BH//CK

BH\(\perp\)AC

Do đó: CK\(\perp\)CA

Ta có: BK//CH

AB\(\perp\)CH

Do đó; BK\(\perp\)BA

c: Gọi O là giao điểm của HI và BC

BC là đường trung trực của HI

=>BC\(\perp\)HI tại O và O là trung điểm của HI

Xét ΔHIK có

O,M lần lượt là trung điểm của HI,HK

=>OM là đường trung bình của ΔHIK

=>OM//IK

=>IK//BC

Xét ΔCHI có

CO là đường cao

CO là đường trung tuyến

Do đó: ΔCHI cân tại C

=>CH=CI

mà CH=BK

nên BK=CI

Xét tứ giác BCKI có

BC//KI

BK=CI

Do đó: BCKI là hình thang cân

a/

DE//BC (gt) nên

\(\widehat{ADE}=\widehat{ABC}\) (Góc so le trong)

\(\widehat{AED}=\widehat{ACB}\) (Góc so le trong)

\(\widehat{ABC}=\widehat{ACB}\) (Góc ở đáy tg cân)

\(\Rightarrow\widehat{ADE}=\widehat{AED}\) => tg AED cân tại A => AE=AD

b/

DE//BC (gt) => DEBC là hình thang

Xét tg ABE và tg ADC có

AE=AD (cmt); AB=AC (cạnh bên tg cân)

\(\widehat{BAE}=\widehat{CAD}\) (Góc đối đỉnh)

=> tg ABE = tg ACD (c.g.c) => BE=CD

=> DEBC là hình thang cân

a: Ta có: ED//BC

=>\(\widehat{ADE}=\widehat{ABC}\)(hai góc so le trong) và \(\widehat{AED}=\widehat{ACB}\)(hai góc so le trong)

mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)

nên \(\widehat{ADE}=\widehat{AED}\)

=>AE=AD

b: Ta có: AD+AB=BD

AE+AC=CE

mà AD=AE và AB=AC

nên BD=CE

Xét tứ giác BCDE có

BC//DE

BD=CE

Do đó: BCDE là hình thang cân

\(\dfrac{8x^4y^3+24x^3y^2-2x^2y^2}{4x^2y^2}\)

\(=\dfrac{8x^4y^3}{4x^2y^2}+\dfrac{24x^3y^2}{4x^2y^2}-\dfrac{2x^2y^2}{4x^2y^2}\)

\(=2x^2y+6x-\dfrac{1}{2}\)