Trong mặt phảng tọa độ oxy cho parapol (P):y=-x^2 và đường thẳng (d):y=(2-m)x+m-3
a) Tìm m để (d) cắt (P) tại 2 điểm phân biệt có hoành độ thỏa mãn(hình ảnh) 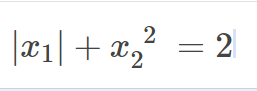
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HB=\sqrt{15^2-9^2}=12\left(cm\right)\)
ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>\(BC=2\cdot BH=24\left(cm\right)\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{15^2+15^2-24^2}{2\cdot15\cdot15}=\dfrac{-7}{25}\)
=>\(sinBAC=\sqrt{1-\left(-\dfrac{7}{25}\right)^2}=\sqrt{1-\dfrac{49}{625}}=\dfrac{24}{25}\)
Xét ΔABC có \(\dfrac{BC}{sinBAC}=2R\)
=>\(2R=24:\dfrac{24}{25}=25\)
=>R=12,5(cm)

A = (\(\dfrac{1}{x-\sqrt{x}}\) + \(\dfrac{1}{\sqrt{x}+1}\)) : \(\sqrt{x}\) + \(\dfrac{1}{x-2\sqrt{x}+1}\)
Có phải đề bài như này không em?

Để chứng minh rằng (2 + \frac{3}{2} + \frac{5}{2}) là số vô tỉ, ta cần chứng minh rằng tổng này không thể biểu diễn dưới dạng một tỉ số của hai số nguyên. Để làm điều này, ta có thể chứng minh bằng phản chứng, giả sử rằng tổng đó là một số tỉ.
nhớ tick cho mik nhé

Bài toán này liên quan đến hình học và tính toán trên đường tròn. Để giải bài toán này, chúng ta cần sử dụng các công thức hình học cơ bản.
a) Để tính khoảng cách từ điểm O đến đường AB, ta có thể sử dụng công thức tính khoảng cách từ một điểm đến một đường thẳng.
b) Để tính số đo cung nhỏ AB, ta cần sử dụng công thức tính độ dài cung trên đường tròn.
c) Để tính diện tích hình bán nguyệt giới hạn bởi dây cung AB và cung nhỏ AB, ta có thể sử dụng công thức tính diện tích hình tròn và hình tam giác.
d) Để tính IA và IB, ta có thể sử dụng định lý cosin trong tam giác vuông và các công thức hình học khác.

\(B=\left(\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1-\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}\right)^2\)
\(=\left(a+2\sqrt{a}+1\right)\left(\dfrac{1}{1+\sqrt{a}}\right)^2\)
\(=\left(\sqrt{a}+1\right)^2.\dfrac{1}{\left(\sqrt{a}+1\right)^2}=1\)
\(C=\dfrac{\sqrt{x}-\sqrt{y}}{xy\sqrt{xy}}:\left[\left(\dfrac{x+y}{xy}\right).\dfrac{1}{\left(\sqrt{x}+\sqrt{y}\right)^2}+\dfrac{2}{\left(\sqrt{x}+\sqrt{y}\right)^3}.\left(\dfrac{\sqrt{x}+\sqrt{y}}{\sqrt{xy}}\right)\right]\)
\(=\dfrac{\sqrt{x}-\sqrt{y}}{xy\sqrt{xy}}:\left[\dfrac{x+y}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}+\dfrac{2}{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)^2}\right]\)
\(=\dfrac{\sqrt{x}-\sqrt{y}}{xy\sqrt{xy}}:\left[\dfrac{x+y}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}+\dfrac{2\sqrt{xy}}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}\right]\)
\(=\dfrac{x-y}{xy\sqrt{xy}}:\left[\dfrac{x+y+2\sqrt{xy}}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}\right]\)
\(=\dfrac{x-y}{xy\sqrt{xy}}:\left[\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{xy\left(\sqrt{x}+\sqrt{y}\right)^2}\right]=\dfrac{x-y}{xy\sqrt{xy}}.xy\)
\(=\dfrac{x-y}{\sqrt{xy}}\)
\(=\dfrac{2-\sqrt{3}-\left(2+\sqrt{3}\right)}{\sqrt{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}}=\dfrac{-2\sqrt{3}}{\sqrt{4-3}}=-2\sqrt{3}\)
\(A=\dfrac{\sqrt{2}\left(1+\sqrt{5}\right)}{2+\sqrt{6+2\sqrt{5}}}+\dfrac{\sqrt{2}\left(1-\sqrt{5}\right)}{2-\sqrt{6-2\sqrt{5}}}\)
\(=\dfrac{\sqrt{2}\left(1+\sqrt{5}\right)}{2+\sqrt{\left(\sqrt{5}+1\right)^2}}+\dfrac{\sqrt{2}\left(1-\sqrt{5}\right)}{2-\sqrt{\left(\sqrt{5}-1\right)^2}}\)
\(=\dfrac{\sqrt{2}\left(1+\sqrt{5}\right)}{2+\sqrt{5}+1}+\dfrac{\sqrt{2}\left(1-\sqrt{5}\right)}{2-\left(\sqrt{5}-1\right)}\)
\(=\dfrac{\sqrt{2}\left(1+\sqrt{5}\right)}{3+\sqrt{5}}+\dfrac{\sqrt{2}\left(1-\sqrt{5}\right)}{3-\sqrt{5}}\)
\(=\sqrt{2}\left(\dfrac{\left(1+\sqrt{5}\right)\left(3-\sqrt{5}\right)+\left(1-\sqrt{5}\right)\left(3+\sqrt{5}\right)}{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}\right)\)
\(=\sqrt{2}.\left(\dfrac{-4}{9-5}\right)=-\sqrt{2}\)

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{13^2-5^2}=12\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot13=5\cdot12=60\)
=>\(AH=\dfrac{60}{13}\left(cm\right)\)
Xét ΔAHB vuông tại H có
\(cosBAH=\dfrac{AH}{AB}=\dfrac{60}{13}:5=\dfrac{12}{13}\)
nên \(\widehat{BAH}\simeq23^0\)

Ta có pt hoành độ giao điểm là:
\(-x^2=\left(2-m\right)x+m-3\\ \Leftrightarrow x^2+\left(2-m\right)x+m-3=0\)
Để pt có nghiệm phân biệt thì:
\(\Delta=\left(2-m\right)^2-4\cdot1\cdot\left(m-3\right)\\ =4-4m+m^2-4m+12=m^2-8m+16=\left(m-4\right)^2>0\)
`=>m-4<>0<=>m<>4`
Ta có: `a+b+c=1+(2-m)+(m-3)=0`
\(=>x_1=1\)
Theo vi-ét ta có: \(x_1+x_2=m-2=>x_2=m-2-x_2=m-2-1=m-3\)
\(\left|x_1\right|+x_2^2=2\\ =>1+\left(m-3\right)^2=2\\< =>\left(m-3\right)^2=2-1=1\\ < =>\left[{}\begin{matrix}m-3=1\\m-3=-1\end{matrix}\right.\\ < =>\left[{}\begin{matrix}m=1+3=4\left(ktm\right)\\m=-1+3=2\left(tm\right)\end{matrix}\right.\)
Vậy: ...