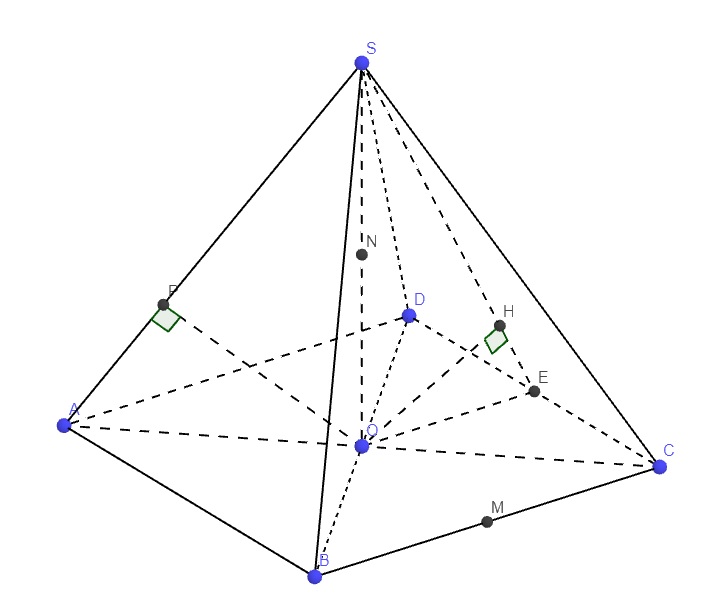
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, AD = a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp I.BCD biết I là trung điểm SD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số tháng tối thiểu để ông An có tổng cộng là 600 triệu đồng là x(tháng)
(ĐK: x>0)
Sau 1 tháng, số tiền ông An có được là \(500\cdot\left(1+0,7\%\right)\left(triệuđồng\right)\)
=>Sau x tháng, số tiền ông An có được là:
\(500\left(1+0,7\%\right)^x\left(triệuđồng\right)\)
Theo đề, ta có:
\(500\left(1+0,7\%\right)^x=600\)
=>\(\left(1+0,7\%\right)^x=1,2\)
=>\(x=log_{1+0,7\%}1,2\simeq26\)
Vậy: ông An cần gửi ít nhất 26 tháng

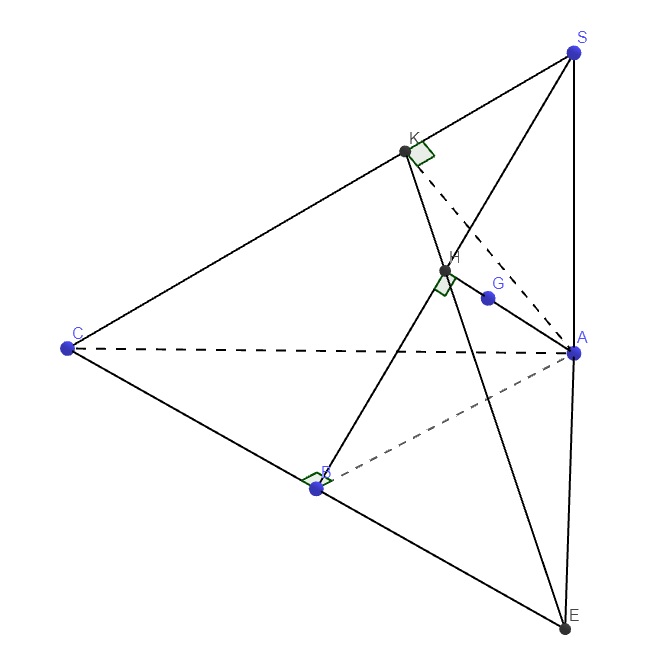
K thuộc SC nên (KBC) cũng là (SBC)
Từ A kẻ \(AH\perp SB\) (H thuộc SB)
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AH\)
\(\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH=d\left(A;\left(KBC\right)\right)=\dfrac{a}{\sqrt{2}}\)
Hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow SA=\dfrac{AH.AB}{\sqrt{AB^2-AH^2}}=a\)
(tới đây nếu sử dụng kiến thức 12 tọa độ hóa thì bài toán được giải quyết nhanh gọn, còn làm kiểu hình thuần 11 hơi dài)
\(\Rightarrow SA=AB\Rightarrow\Delta SAB\) cân tại A \(\Rightarrow AH\) đồng thời là trung tuyến \(\Rightarrow G\) thuộc AH
\(\Rightarrow\left(AGK\right)\) trùng mặt phẳng \(\left(AHK\right)\)
Trong mp (SBC), nối HK cắt BC kéo dài tại E
\(\Rightarrow AE=\left(ABC\right)\cap\left(AGK\right)\) (1)
Theo cmt \(AH\perp\left(SBC\right)\Rightarrow AH\perp SC\Rightarrow SC\perp\left(AGK\right)\Rightarrow SC\perp AE\)
\(SA\perp\left(ABC\right)\Rightarrow SA\perp AE\)
\(\Rightarrow AE\perp\left(SAC\right)\) (2)
(1);(2) \(\Rightarrow\widehat{CAK}\) là góc giữa (ABC) và (AGK)
Hệ thức lượng: \(AK=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=\dfrac{a\sqrt{6}}{3}\)
\(\Rightarrow cos\widehat{CAK}=\dfrac{AK}{AC}=\dfrac{\sqrt{3}}{3}\)

\(f\left(x\right)=\dfrac{2x+3}{x-2}\)
=>\(f'\left(x\right)=\dfrac{\left(2x+3\right)'\left(x-2\right)-\left(2x+3\right)\left(x-2\right)'}{\left(x-2\right)^2}\)
=>\(f'\left(x\right)=\dfrac{2\left(x-2\right)-2x-3}{\left(x-2\right)^2}=\dfrac{-7}{\left(x-2\right)^2}\)
\(f'\left(4\right)=\dfrac{-7}{\left(4-2\right)^2}=-\dfrac{7}{4}\)

Em kiểm tra lại đề \(BC\) cắt \(\left(AB'C\right)\) tại C nên giữa chúng ko có khoảng cách
Hay là mặt phẳng \(\left(AB'C'\right)\)?

a.
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp BD\\BD\perp AC\left(\text{hai đường chéo hv}\right)\end{matrix}\right.\)
\(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp SA\)
Mà \(SA\perp OP\left(gt\right)\)
\(\Rightarrow SA\perp\left(PBD\right)\)
b.
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\Rightarrow OC=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow SO=\sqrt{SC^2-OC^2}=\dfrac{a\sqrt{14}}{2}\)
\(V=\dfrac{1}{3}SO.AB.AD=\dfrac{a^3\sqrt{14}}{6}\)
c.
Chắc đề ghi nhầm, (SCD) là mặt chứ đâu phải đường
Gọi E là trung điểm CD, tam giác SCD cân tại S \(\Rightarrow SE\perp CD\)
Tam giác OCD cân tại O \(\Rightarrow OE\perp CD\)
\(\Rightarrow CD\perp\left(SOE\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SEO}\) là góc giữa (SCD) và (ABCD)
\(OE=\dfrac{1}{2}AD=\dfrac{a}{2}\) (đường trung bình)
\(tan\widehat{SEO}=\dfrac{SO}{OE}=\sqrt{14}\Rightarrow\widehat{SEO}\approx75^02'\)
d.
\(\left\{{}\begin{matrix}AO\cap\left(SCD\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)\)
Trong tam giác vuông SEO, từ O kẻ \(OH\perp SE\) (1)
Theo cmt, \(CD\perp\left(SEO\right)\Rightarrow CD\perp OH\) (2)
(1);(2) \(\Rightarrow OH\perp\left(SCD\right)\Rightarrow OH=2\left(O;\left(SCD\right)\right)\)
Hệ thức lượng:
\(OH=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{210}}{30}\)
\(\Rightarrow d\left(A;\left(SCD\right)\right)=2OH=\dfrac{a\sqrt{210}}{15}\)
//Ko hiểu đề cho 2 điểm M và N làm gì, ko liên quan gì đến toàn bộ 4 câu hỏi luôn