Bài học cùng chủ đề
- Bài 1: Xét tính đơn điệu của hàm số trên một khoảng xác định (P1)
- Bài 1: Xét tính đơn điệu của hàm số trên một khoảng xác định
- Bài 1: Xét tính đơn điệu của hàm số trên một khoảng xác định (P2)
- Bài 2: Các bài toán biến thiên chứa tham số (P1)
- Bài 2: Các bài toán biến thiên chứa tham số (P2)
- Bài 2: Các bài toán biến thiên chứa tham số
- Bài 3: Các bài toán biến thiên chứa hàm hợp
- Bài 3: Các bài toán biến thiên chứa hàm hợp
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Hàm số y=f(x)
- nghịch biến
- đồng biến
Hàm số y=f(x)
- nghịch biến
- đồng biến
Cho hàm số y=f(x) đồng biến trên khoảng (0;+∞), khẳng định nào sau đây đúng?
Tập xác định của hàm số y=−x4+8x2+6 là
Hàm số y=−x4+8x2+6 có đạo hàm

Cho đa thức (y′=−4x3+16x) bảng xét dấu như trên, trong khoảng (left(2;+inftyight)) , (y′) mang dấu
- dương
- âm
(Chú ý: Quy tắc xét dấu đa thức (gleft(xight)=ax3+bx2+cx+d) : dấu của khoảng bên phải nghiệm lớn nhất cùng dấu với hệ số (a).)
Tập xác định của hàm số y=−x+12x+1 là
Đạo hàm của hàm số y=−x+12x+1 là
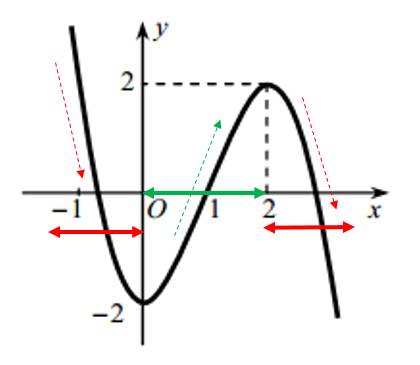
Cho hàm số (y=fleft(xight)) có đồ thị như hình trên, đồ thị hàm số đi lên theo chiều từ trái qua phải trong khoảng
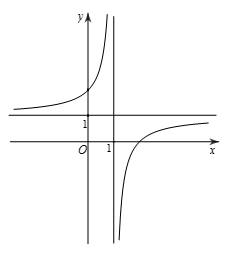
Cho hàm số (y=fleft(xight)) có đồ thị như hình vẽ trên, hàm số không liên tục tại (x=)
- 1
- 0
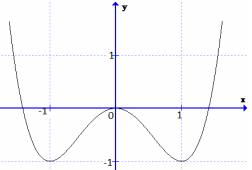
Cho đồ thị hàm số (y=fleft(xight)) như hình trên. Các khẳng định sau là đúng hay sai?
(Nhấp vào dòng để chọn đúng / sai)| Hàm số nghịch biến trên (left(−infty;−1ight).) |
|
| Hàm số nghịch biến trên (left(1;+inftyight).) |
|
| Hàm số đồng biến trên (left(−1;1ight).) |
|
| Hàm số đồng biến trên (left(2;+inftyight).) |
|
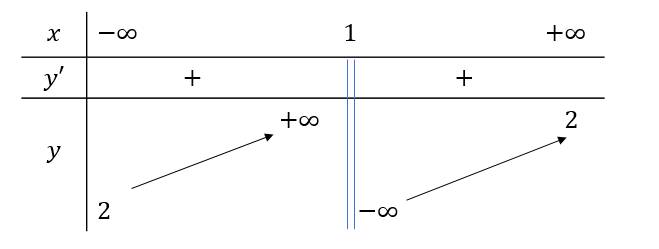
Hàm số (y=fleft(xight)) có bảng biến thiên như hình vẽ trên không liên tục tại (x=)
- 2
- 1
Cho hàm số y=f(x) có bảng biến thiên như sau:
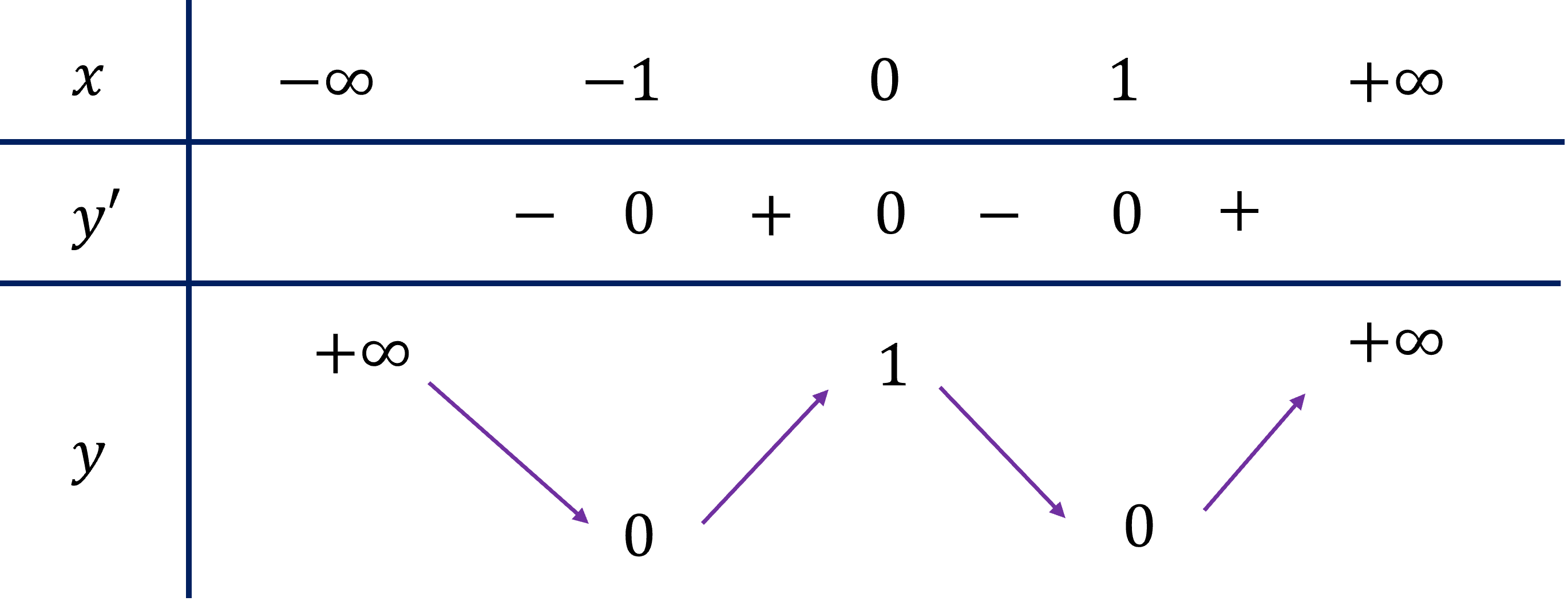
Hàm số đồng biến trên khoảng nào dưới đây?
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Xin
- chào mừng các em đã quay trở lại vì quá
- Học Toán lớp 12 của trang web oml.vn
- Hôm nay chúng ta sẽ cùng nhau tìm hiểu
- chuyên đề tính đơn điệu của hàm số
- từ trước khi liền gửi trên đề này thì cô
- sẽ nhắc lại một số nội dung lí thuyết mà
- chúng ta đã học ở các video trước
- Hà Nội dung thứ nhất là định nghĩa hàm
- số đồng biến nghịch biến trên một khoảng
- anh em Hãy trả lời câu hỏi sau
- Ừ vậy tao nói hàm số FX đồng biến trên
- khoảng ca nhiều với mọi cặp x1 x2 thuộc
- ca mà X1 nhỏ hơn X2 thì fx1 nhỏ thuộc
- fx2 tương tự hàm số FX được gọi là
- nghịch biến trên khoảng ca Nếu với mọi
- cặp x1 x2 thuộc ca mà X1 nhỏ hơn X2 thì
- fx1 lớn hơn FX 2
- Hà Nội dung thứ hai là quy tắc xét tính
- đơn điệu của hàm số
- quy tắc này bao gồm 4 bước Bước đầu tiên
- tìm tập xác định thức thứ hai ra tính
- đạo hàm và các nhiệm xy mà tại đó đạo
- hàm bằng 0 hoặc là không xác định bước
- tiếp theo sắp xếp các điểm xy theo thứ
- tự tăng dần Và từ đó tăng lực bảng xếp
- tấu của Y Faith và bước cuối cùng chúng
- ta kết luận
- ông bà Để hiểu hơn về quy tắc này thì
- chúng ta sẽ cùng nhau đi đến ví dụ đầu
- tiên
- xem xét sự đồng biến nghịch biến của hàm
- số y bằng trừ x mũ 4 + 8 x bình phương
- cộng 6 chúng ta sẽ thực hiện lần lượt
- theo 4 bước đầu tiên là tìm cực xác định
- đối với khác hàm đa thức thì được xác
- định là d = r
- Anh Đức tiếp theo các tỉnh đạo hàm và
- xác định các hiểm
- xy Vậy theo các em thì đạo hàm của hàm
- số này là gì
- các bác khỏi phải bằng trừ 4 x mũ 3 cộng
- 16x
- em nhận thấy là y phẩy luôn xác định với
- mọi x vậy ta giải đi phẩy bằng không
- Phân tích đa thức thành nhân tử được y
- bằng trừ 4 x x trừ 2 nhân x + 2 = 0
- tìm đường x = -2 x bằng 0 hoặc x = 2
- anh cứ theo ta lập bảng xét dấu của y
- phẩy
- Ừ chú ý khi lập bảng xét dấu của y phẩy
- từ đầu tiên ta sắp xếp các điểm xy theo
- thứ tự tăng dần từ trái qua phải ở đây
- ta có 3 nghiệm là - 20 và 2
- a tiếp theo phép xử của y phẩy
- Ừ vậy thì các em hãy nhớ lại khi các sếp
- dấu đa thức đó là giấu cục khoảng bên
- phải nhận lớn nhất thì sẽ cùng dù với hệ
- số a
- ở đây là khoảng bên phải nhiệm lớn nhất
- vì vậy phẩy bằng trừ 4 x mũ 3 cộng 16x
- cụ thể a = -4 Nghĩa là a âm vậy ta có
- dấu của khoảng này là số âm
- a tiếp theo do y phẩy bằng không có 3
- nghiệm phân biệt vì vậy dấu của y phẩy
- sẽ đổi liên tục khi đi qua 3 nhiệm này
- để ta hoàn thành được xấu của các khoảng
- còn lại
- và bước cuối cùng vì chúng ta kết luận
- dựa vào dấu của iface
- Anh nhận thấy trên từng khoảng từ âm có
- cùng biến - 2a và khoảng không đến hay
- đi phẩy lớn hơn không Vì vậy ta kết luận
- là hàm số đồng biến trên từng khoảng từ
- âm vô cùng đến - 2 và không đến hai
- tương tự thì hàm số nghịch biến trên
- từng khoảng về - 2 đến không và 2 đến
- dương vô cùng do ý phẩy nhỏ thu không
- trên các khoản này
- khi kết thúc ví dụ đầu tiên ở đây là
- chúng ta cùng nhau bước sang ví dụ thứ 2
- Cho hàm số y = 2x cộng 1 trên x cộng 1
- để khẳng định nào sau đây là đúng
- Ừ từ ngắn a-hàm Sống biến trên khoảng từ
- âm vô cùng đến một phương án b hàm số
- nghịch biến trên khoảng từ âm vô cùng
- đến - một Hương án c hàm số đồng biến
- trên khoảng 1 đến dương vô cùng và
- phương án b hàm số đồng biến trên khoảng
- -1 đến dương vô cùng
- Ừ từ ví dụ này thì chúng ta cũng sẽ làm
- tương tự về ví dụ đầu tiên
- Nhà nước đầu tiên cao tìm tập xác định
- vậy theo các em thì cần xác định của hàm
- số này là gì
- Cho hàm số y = 2x + 1 trên trừ x cộng 1
- xác định khi trừ x cộng 1 khác không
- Nghĩa là X1 vì vậy ta phép d = r - 1
- ở nước thứ hai ta tính y phẩy
- A phẩy = ba trên trừ x cộng 1 tất cả
- bình phương
- cho và nhận thấy là y tẩy lớn hơn 0 với
- mọi x H1 vì vậy đến đây ta kết luận được
- hàm số đồng biến trên từng khoảng từ âm
- vô cùng đến một và một đến dương vô cùng
- Khi được chiếu với các phương án này đã
- cho thì ta sẽ loại được luôn thư ngắn A
- và phương án b do hàm số nghịch biến sai
- vậy còn thương án c hàm số đồng biến
- trên khoảng 1 bình dương vô cùng gắn
- Đúng vậy ta chọn C
- ạ Và bây giờ thì chúng ta sẽ cùng bước
- vào bài đầu tiên của chuyên đề này bài 1
- xét tính đơn điệu của hàm số trên mặt
- phẳng đã cho
- em về bài học mẹ thì ta sẽ cùng nhau
- nghiên cứu 4 dạng toán
- ở dạng Đầu Tiên Biết đồ thị hàm số y
- bằng FX xét tính đơn điệu của hàm số này
- trên một khoảnh đã cho
- a Đối với dạng toán này thì phương pháp
- làm của chúng ta là chú ý vào những cái
- khoảng mà đồ thị hàm số đi lên và đi
- xuống
- sau khi đồ thị hàm số FX đi lên theo
- chiều từ trái sang phải trong một khoảng
- a đến b thì ta nói là hàm số đồng biến
- trên khoảng a đến b
- A và tương tự ta nói hàm số nghịch biến
- trên khoảng từ A đến B nếu đồ thị hàm số
- FX đi xuống cũng theo chiều từ trái qua
- phải trong khoảng a đến b
- à mà Để hiểu hơn về dạng toán này thì
- chúng ta sẽ cùng bước vào ví dụ thứ nhất
- ví dụ 1.1 cho đồ thị hàm số như hình vẽ
- dưới
- vậy Câu hỏi đặt ra làm số đã cho đồng
- biến trên khoảng nào dưới đây tư ngắn a
- khoảng từ âm vô cùng đến không phương án
- b khoảng 0 đến 2 dự án C là khoảng một
- bình dương vô cùng hương lắm d khoảng từ
- 2 đến 2
- chủ đề bài nhắc đến cụm từ đồng biến vì
- vậy chúng ta sẽ chú ý vào những cái
- khoảng mà hàm số đi lên theo chiều từ
- trái sang phải và quan sát đồ thị hàm số
- y ta thuế trên khoảng từ 0 đến 2 đồ thị
- hàm số đi lên và ta gói hàm số đồng biến
- trên khoảng này tương tự trên từng
- khoảnh thì âm vô cùng đến không và 2 đến
- dương vô cùng đồ thị hàm số đi xuống
- cũng theo chiều từ trái qua phải người
- ta nói hàm số nghịch biến trên từng
- khoảng từ âm có cùng đến không và 2 đến
- dương vô cùng
- đã quay trở lại với các phương án tư
- ngắn A
- là từ âm vô cùng đến không Đây là phương
- án sai vì như chúng ta đã khẳng định
- người trước thì từ khoảng từ âm cùng đến
- không làm số nghịch biến tương ngắn C
- Ừ chắc khoảng từ 1 đến dương vô cùng thì
- chúng ta nhận thấy là khoảng từ 1 đến 2
- hàm số đồng biến còn khoảng thứ hai đến
- dương vô cùng là hàm số nghịch biến
- à Vì vậy là phương án c cũng là phương
- án sai
- đa phương án đề khoảng từ thứ 2 đến hai
- từ án này cũng sai tương tự về phương án
- c còn lại phương án b là phương án đúng
- là chọn B
- cho ví dụ tiếp theo ví dụ 1.2 cho đồ thị
- hàm số như hình vẽ dưới
- Cho hàm số đã cho đường biến trên khoảng
- nào dưới đây tư ngắn a khoảng từ âm vô
- cùng đến 1
- a b âm vô cùng đến dương vô cùng C từ âm
- vô cùng đến một hợp với khoảng một bình
- dương vô cùng phương án b và r - 1
- chủ đề bài cũng nhắc đến cụm từ đồng
- biến vì vậy là ta sẽ chú ý những khoảnh
- mà đồ thị hàm số đi lên trên
- khi quan sát hình vẽ thì ta nhận thấy
- trên từng khoảng từ âm vô cùng đến một
- và một điểm dương vô cùng thì đồ thị hàm
- số đi lên theo chiều từ trái qua phải để
- ta nói hàm số đồng biến
- anh ở đây
- cho nên chú ý khi kết luận tính đơn điệu
- của hàm số ta kết luận sự đồng biến và
- nghịch biến trên từng khoảng xác định Vì
- vậy Hương án c và phương án b chúng ta
- lại được luôn vì sử dụng ký hiệu hợp và
- ký hiệu - tập hợp
- số còn lại phim ngắn A và phương án b
- khi quan sát hình vẽ ta thấy tại điểm x
- = 1 hàm số không liên tục vì vậy thương
- án b cũng là phương án sai vậy chúng ta
- cho A hàm số đã cho đồng biến trên
- khoảng từ âm vô cùng đến 1
- khi kết thúc dạng toàn thứ nhất Chúng ta
- cùng bước sang dạng toán tiếp theo tiết
- bảng biến thiên của hàm số và xét tính
- đơn điệu của hàm số này trên một Quảng
- Ngãi cho
- ẩm thực chất thì dạng toán này cũng
- tương tự với dạng toán trước khi mà ta
- cách điệu đồ thị hàm số thành những
- đường cong đường gấp khúc
- à Vì vậy là phương pháp giải của chúng
- ta cũng sẽ tương ngực nghĩa là chúng ta
- quan sát những khoảnh và đồ thị hàm số
- hay còn gọi là đường cong đi lên hay là
- đi xuống
- Cho hàm số đó được gọi là đồng biến trên
- khoảng ca Nếu mà đường cong đi lên theo
- chiều từ trái qua phải
- anh nói tương tự thì hàm số đó nghịch
- biến trên khoảng ca Nếu mà đường cong đi
- xuống cũng theo chiều từ trái sang phải
- A và ví dụ đầu tiên các dạng toán này ví
- dụ 2.1
- a Cho hàm số xác định và liên tục trên R
- và có bảng biến thiên như hình vẽ ở dưới
- Câu hỏi đặt ra là hàm số nghịch biến
- trên khoảng nào dưới đây Các có bốn
- phương án a âm vô cùng đến - 1B -1 đến 1
- C từ 1 đến dương vô cùng và phương án D
- thì trường 1 đến 2
- à vì bà nhắc về những cụm từ nghịch biến
- vì vậy chúng ta sẽ chú ý và những cái
- khoảng mà đường cong đi xuống
- à con dắt bảng biến thiên ta nhận thấy
- trên khoảng từ -1 đến 1 đồ thị hàm số đi
- xuống theo chiều từ trái qua phải nghĩa
- là hàm số nghịch biến
- A và tương tự thì trên mỗi khoảng từ âm
- cùng đến - 1 và 1 đến dương vô cùng
- hàng xóm đồng biến
- khi quan sát các phương án tư ngắn A từ
- ông cùng đến - 1
- Ừ chắc khoảng từ âm vô cùng đến - một đồ
- thị hàm số đi lên nghĩa là hàm số đồng
- biến các loại hương án a
- từ tương tự cho phương án c khoảng từ 1
- đến dương vô cùng hàng số cũng đồng biến
- tương án c chúng ta loại
- a tiếp tục cần thơ ngắn b là phương án B
- đã nhận thấy B khoảng từ -1 đến 1 đồ thị
- hàm số đi xuống nghĩa là hàm số nghịch
- biến
- vì vậy ta chọn phương án b là phương án
- đúng cho ví dụ 2.1
- cho ví dụ tiếp theo ví dụ 2.2
- a Cho hàm số y bằng FX có bảng biến
- thiên như hình vẽ dưới
- vì vậy hàm số đồng biến trên khoảng nào
- dưới đây tương là na thì âm có cùng đến
- một hợp với khoảng một bình dương vô
- cùng hương án b r - 1 tương án C từ âm
- vô cùng đến một và một đến dương vô cùng
- tương án b từ âm cùng đến 2 và 2 đến
- Gương vô cùng
- khi quan sát bảng biến thiên vì ta nhận
- thấy là xin lỗi khoảng từ Ông Cù đến một
- và một đến dương vô cùng thì đồ thị hàm
- số đi lên theo chiều từ trái qua phải
- hết hàm số đồng biến
- Nghe tiếng đàn A và phương án b thì
- chúng ta loại theo như cô đã chú ý ở
- trước thì chúng ta không sử dụng ký hiệu
- hợp hay là - tập hợp để kết luận sự đồng
- biến nghịch biến của hàm số và chỉ kết
- luận tính đơn điệu của nó trên từng
- khoảng xác định còn phương án c và
- phương án đê thì chúng ta chọn phương án
- c thì âm cùng đến một và khoảng từ 1 đến
- dương vô cùng
- cho ví dụ cuối cùng ví dụ 2.3 Cho hàm số
- có bảng biến thiên như hình ở dưới
- Ừ vậy câu hỏi là hàm số nghịch biến trên
- khoảng nào dưới đây
- chị thơ ngắn A Quảng từ âm vô cùng đến
- trường một phương án b khoảng từ -1 đến
- 1 tương án C không đến dương vô cùng và
- phương án đê thì chị một tín không
- khi các em chú ý ký hiệu gạch ở bảng
- biến thiên có nghĩa là hàm số
- y và y phẩy không xác định tại x = 0
- a tiếp theo do để bày yêu cầu hàm số
- nghịch biến trên khoảng nào vì vậy là
- chúng ta sẽ chú ý những khoảnh mà đồ thị
- hàm số dân xúm
- Anh nhận thấy trên mũi khoảng từ -1 đến
- 0 và không đến một thì đồ thị hàm số đi
- xuống nghĩa là hàm số nghịch biến
- khi quan sát các phương án phương án a
- từ âm vô cùng đến - 1
- cho đồ thị hàm số đi lên theo chiều từ
- trái qua phải vậy trên khoảng từ âm vô
- cùng đến trường một hàm số đồng biến ra
- loại hương án a ta tiếp tục phương án b
- khoảng từ -1 đến 1
- thế nhưng cô đã nói thì tại x = 0 hàm số
- không xác định
- Ừ thì vậy cũng không xác định Vì vậy
- chúng ta loại phương án b
- a tiếp theo phương án c khoảng từ 0 đến
- dương vô cùng
- Anh nhận thấy trên khoảng từ 1 đến dương
- vô cùng
- cho đồ thị hàm số đi lên nghĩa là hàm số
- đồng biến vì vậy Là khoảng từ 0 đến
- dương vô cùng cũng nhạc say
- vì vậy còn phương án D thì -1 đến 0
- Hình như là phương án đúng cho ví dụ 2.3
- vì vậy chúng ta đã cùng nhau nghiên cứu
- xong dạng toàn thứ nhất là dạng toán thứ
- hai Còn hai dặm còn lại thì ta sẽ học
- trong video tiếp theo cảm ơn các em và
- hẹn gặp lại các em trong các bài giảng
- tiếp theo


Bạn có thể đánh giá bài học này ở đây