Bài học cùng chủ đề
- Bài 1: Xét tính đơn điệu của hàm số trên một khoảng xác định (P1)
- Bài 1: Xét tính đơn điệu của hàm số trên một khoảng xác định
- Bài 1: Xét tính đơn điệu của hàm số trên một khoảng xác định (P2)
- Bài 2: Các bài toán biến thiên chứa tham số (P1)
- Bài 2: Các bài toán biến thiên chứa tham số (P2)
- Bài 2: Các bài toán biến thiên chứa tham số
- Bài 3: Các bài toán biến thiên chứa hàm hợp
- Bài 3: Các bài toán biến thiên chứa hàm hợp
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
và x=2 là nghiệm bội
.
Cho hàm số y=f(x) có bảng biến thiên như hình dưới

Phương trình f′(x)=0 có x=−1 là nghiệm bội
- lẻ
- chẵn
- lẻ
- chẵn
Câu 2 (1đ):
0.
Cho hàm số f(x) có bảng xét dấu của f′(x) như sau:

Vậy f′(7)
- <
- >
Câu 3 (1đ):
nghiệm.
Cho hàm số y=f(x) có đồ thị của f′(x) như hình dưới
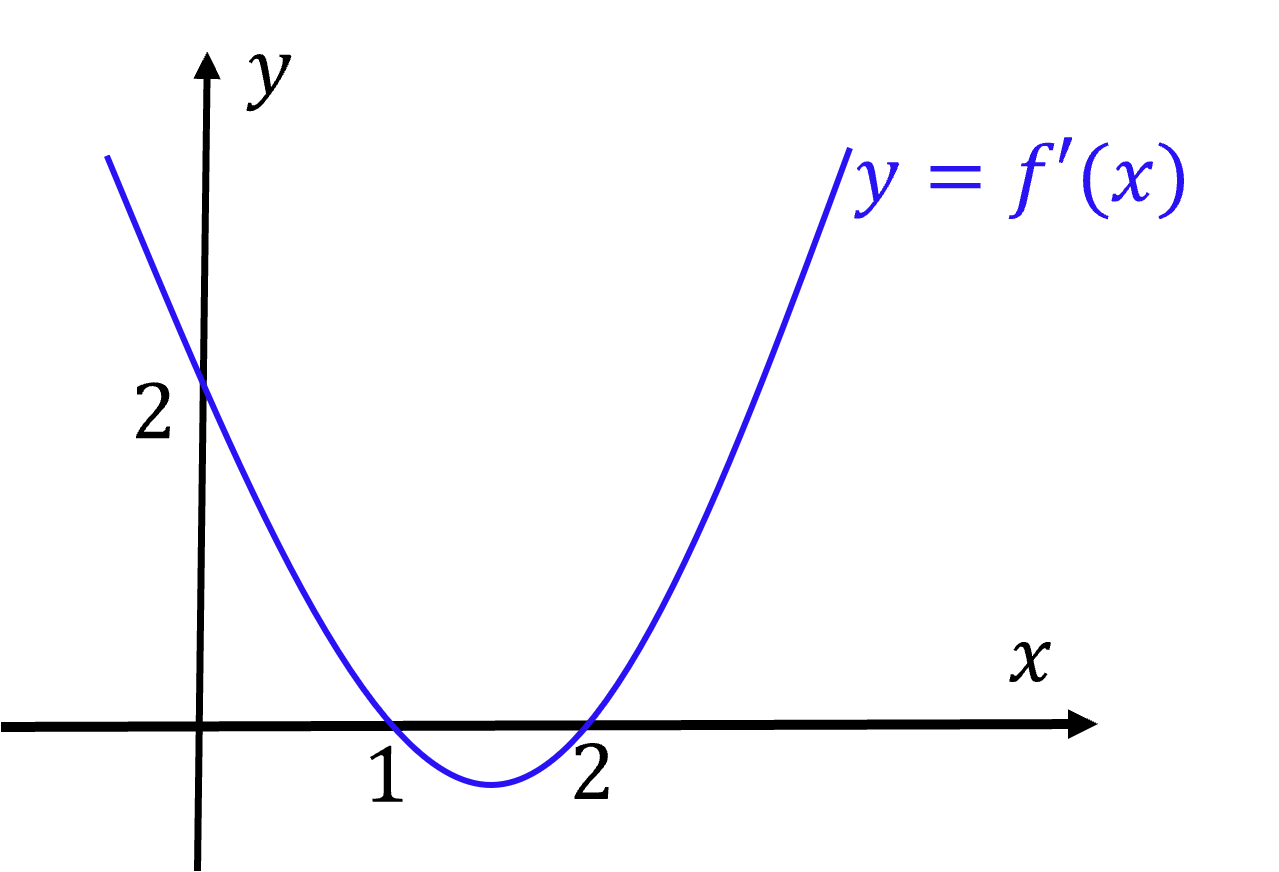
Vậy phương trình f′(x)=0 có
- 3
- 1
- 2
Câu 4 (1đ):
0.
Cho hàm số y=f(x) có đồ thị f′(x) như hình dưới
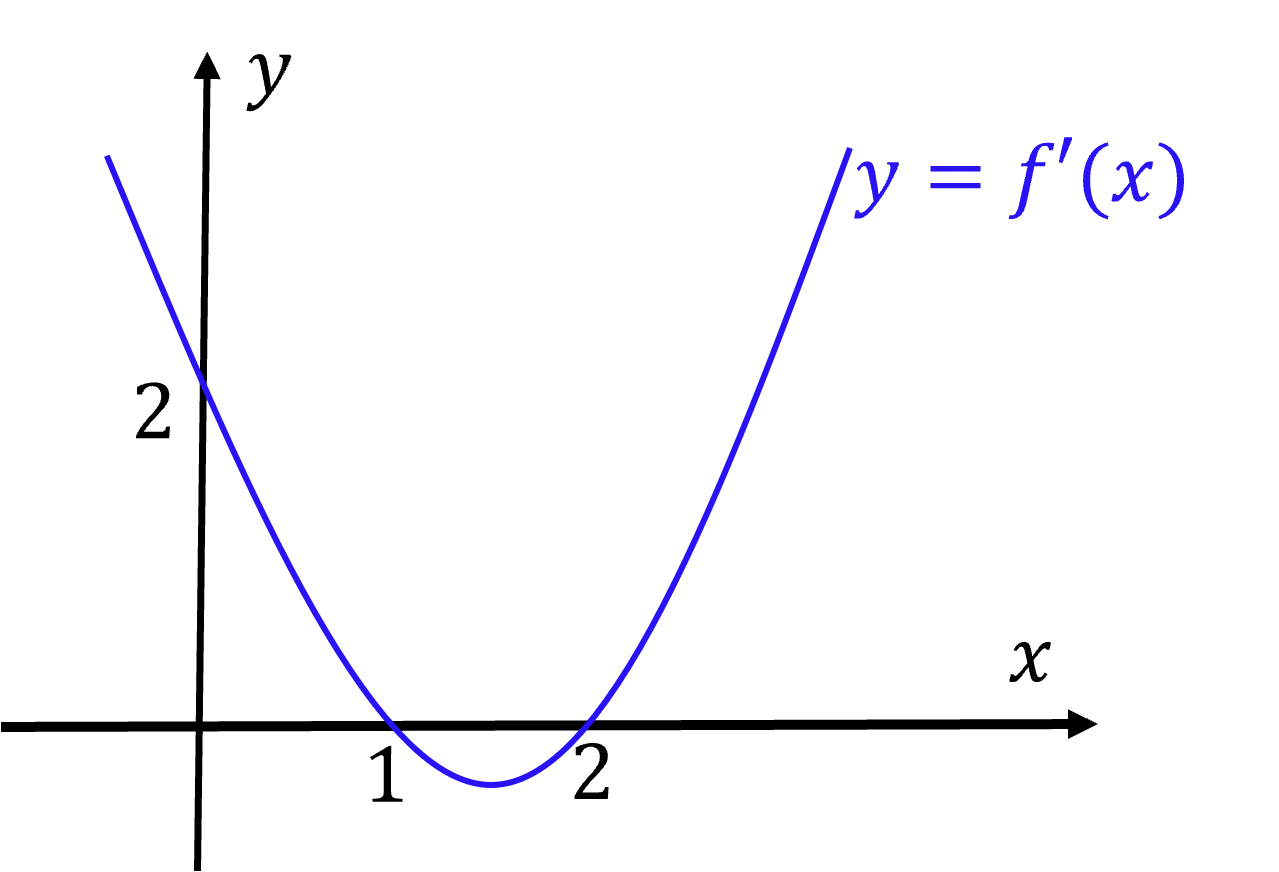
Từ đồ thị ta nhận thấy: f′(0)
- <
- >
Câu 5 (1đ):
0.

Cho đa thức h(x)=−x2+4x có bảng xét dấu như hình bên, trên khoảng (4;+∞) h(x)
- >
- <
Câu 6 (1đ):
Cho hàm số g(x) có bảng xét dấu của g′(x) như hình dưới:
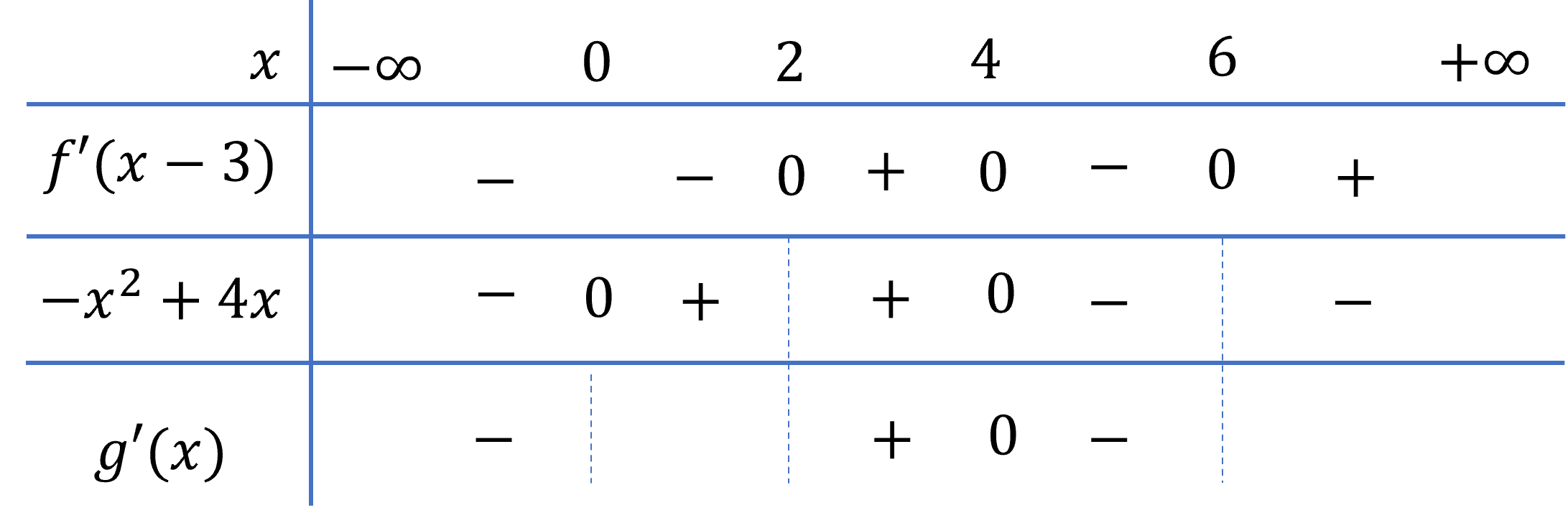
Vậy hàm số g(x) đồng biến trên khoảng
(4;6).
(2;4).
(0;4).
(−∞;2).
Câu 7 (1đ):
Cho x1>25; x2=2 ; x3<45. Thứ tự sắp xếp nào sau đây là đúng?
x1<x2<x3.
x1>x3>x2.
x1>x2>x3.
x1<x3<x2
Câu 8 (1đ):
Đạo hàm của hàm số g(x)=f(x2−2) là
2x.f′(x2−2).
(x2−2)f′(x2−2).
f′(x2−2).
2x.f′(2x).
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Xin
- chào mừng các em quay thử lại với khóa
- học Toán lớp 12 trang web câu lời mời
- chấm vn
- trong bài học ngày hôm nay thì chúng ta
- sẽ tìm hiểu bài cuối cùng trong chuyên
- đề tính đơn điệu hàm số đó là bài 3 các
- bài toán tiền Thiên chứa hàm hợp thế thì
- nhiễm cái bài toán thuộc dạng toán này
- sẽ nằm ở cái mức câu hỏi vận dụng cho
- đến vận dụng cao trong các đề thi và đề
- kiểm tra à
- sau khi mà đề bài yêu cầu chúng ta xét
- tính đơn điệu hàm số GX bằng S của Ox
- biết công thức hàm hoặc là bản chất dấu
- và đồ thị của FX thì chúng ta có cách
- làm tổng quát như sau bước đầu tiên các
- thí nghiệm của SX bằng không khi đó giải
- ra ta được x = a x = b Vân
- tức thứ hai ta tỉnh đạo hàm từ phải x Lý
- do gửi X là hãm hợp xuyên đã áp dụng
- công thức tính đạo hàm của hàm ngực ta
- được giờ về x = u và x x phẩy của Ox và
- giải phương trình cos2x = 0 thì ta sẽ
- được là x bằng 0 hoặc lá f phẩy box bằng
- không với phương trình đầu tiên u và x
- bằng 0 thì khá là đơn giản thì chúng ta
- giải rồi khi đó ta giải các phương trình
- thứ hai này ép dầy cũng ít bằng không
- Bây giờ chúng ta quay ngược sử hạ tên kẻ
- phương trình SX bằng không này từ khi đó
- ích chính là biến vậy ta giải được miếng
- sẽ bằng các giá trị a b vân vân Thế thì
- ở cái phương trình này ép phải của us
- bằng không ta xem ux là biến thì ta sẽ
- phải được vào box bằng a-ox bằng B vân
- vân phải bức thứ ba ta lập bảng xét xử
- của gpx
- sự tích lực bằng xét xử với chúng ta đã
- học rồi Tiên là chúng ta sắp xếp các
- nghiện của người bằng không theo thứ tự
- tăng dần thích một ít hay cho thì tích n
- sau đó xét xử của ông phải x bất tử của
- este X và các thực lại thì ta được số
- của từ X và cuối cùng từ cái bảng xét
- dấu của gpx này thì trường ca đưa ra kết
- luận và bây giờ cô và các em sẽ cùng
- nhau thực hiện một số ví dụ
- ví dụ đầu tiên Cho hàm số y bằng FX có
- bảng xét dấu của SX như hình ở bên và
- câu hỏi đặt ra là hàm số GX bằng ép của
- x bình trừ 2 nghịch biến trên các bảng
- nào
- hãy bước đầu tiên có tìm nghiệm của
- phương trình S = 0 vật nhìn lên bảng xét
- dấu ta thấy S bằng 0 tại hai điểm x = -1
- và x = 2 Tuy nhiên các em chú ý khi đi
- qua nghiệm x = -1 thì f phẩy x không đổi
- dấu vậy x = -1 Hà Nội sẵn là ký hiệu vào
- đây à
- a tiếp theo ta tìm đạo hàm còn số ở xggx
- vẽ bằng đạo hàm của x bình trừ 2 nhân
- gửi s phẩy của x bình trừ 2 chính là =
- 2-x nhân S7 của x bình trừ 2
- Vậy giải phương trình rồi Vỹ bằng không
- ta có 2 X bằng 0 hoặc cửa f phẩy x bình
- trừ 2 bằng 0 tương đương với x bằng 0
- hoặc là x bình trừ 2 = -1 hoặc cách bình
- trừ 2 bằng hai vào đây ta chú ý vào đây
- là nhiệm vụ sẵn này ta có x bằng 0 hoặc
- x bình trừ 2 = -1 nghĩa là x bình bằng 1
- ở đây tích bình bằng 4 Vậy tương đương
- gửi x = 0 x = 1 x bằng trừ 1 x = 2 gọi x
- = -2 x = 1 và x = -1 chính và nhiệm vụ
- sẵn
- và biết rồi chúng ta lập bảng xét xử của
- hàng giờ sĩ
- ta có ích chạy từ âm cô cô bổ sung vô
- cùng ta có 5 nghiệm thứ 2 - 10 12 ở đây
- chú ý một và trừ một là những bộ sẵn thì
- có Khoanh tròn lại bây giờ để xét xấu
- của gợi ý thì ta xếp dấu của Khoảng 2
- đến dương vô cùng đầu tiên vậy ta chọn x
- = 3
- hãy bằng 3 vào Ừ X ở đây đã có phần x =
- 3 thì rồi phải ít sẽ bằng 6X phẩm của x
- bình trừ 2 chỉ là các phẩm vẽ phẩy tại
- bởi thì ta cùng chiếu lên bảng xét dấu
- của SX đề bài đã cho 7 thì thụ khoảng
- thứ hai đến dương vô cùng thế nên là ép
- phải tại 7 sẽ mang dầu Dương và 6X s787
- Dương em với Dương thì chúng ta được
- Dương vậy dấu của khoảng thứ hai đến
- dương vô cùng chính là Dương Quá hay là
- nghiệm bội lẻ là số đầu dấu từ dương
- sang âm Một là nhịp độ sẵn làm sữa giữ
- nguyên dấu không là nghiệp đội lẻ đổi
- dấu thì ông anh
- chưa một lần gục chẵn giữ nguyên dấu và
- cuối cùng đi qua - 2 hạt số đổi dấu từ
- dương sang âm
- và đến đây là chúng ta đã hoàn thành
- được cái bảng xét dấu của cơ thể ít
- người vậy chúng ta kết luận các khoảng
- từ âm vô cùng đến - 2 này và không đến
- hai hàm số GX biến
- có một ví dụ tiếp theo ví dụ 2 Cho hàm
- số y bằng FX có đồ thị của SX như hình
- bên có hỏi đặt ra là số x = f của x trừ
- x bình cộng 11 nghịch biến trên khoảng
- nào trong bốn khoảng dưới đây
- tương tự với ví dụ trước thì bước đầu
- tiên chúng ta sẽ tìm nghiện của f PX
- bằng 0 thì nhìn vào cái đồ thị này chúng
- ta thấy tại hai điểm x = 1 và x = 2 thì
- SX bằng không sau đó tao tính đạo hàm g
- phải ít thì bằng đạo hàm của x trừ x
- bình
- chính là 1 - 2 x nhân gửi f phẩy x bình
- và khi đó của vị bằng không tương đương
- gửi 1 trừ 2 bằng 0 hoặc là ép về có ích
- cho anh bình bằng không tương đương
- người x = 1/2 x trừ x bình = 1 x trừ x
- bình = 2a
- cho phương trình này chính là x bình trừ
- x cộng 1 bằng 0 phương trình x bình trừ
- x cộng 2 bằng không Cả hai đều vô nghiệm
- vì vậy ta có x = 1/2
- ạ
- Bây giờ chúng ta lập bảng xét xử của g
- và x
- x chạy thu âm mưu cùng điện dương vô
- cùng và tại X = 1/2 thìa vệ bằng không
- ạ Bây giờ chúng ta sẽ xét dấu của cái
- khoảng 1/2 đến dương vô cùng đầu tiên
- vậy ta chọn x bằng 1 đi đã ít bằng 1 thì
- g phải x sẽ bằng 1 - 2 là điều trị một
- nhân với s phẩy của không
- Bây giờ chúng ta đối chiếu vào cái đồ
- thị này hết phẩy tại không chính là bằng
- hai vậy phẩy x sẽ mang dấu âm
- vì vậy chúng ta điểm ở đây là xấu âm và
- đi qua 1/2 thìa thấy được số lần xanh
- dương hoàn thành được cái bảng xét dấu
- thì bây giờ chúng ta nhìn vào bảng này
- ta kết luận hàm số GX nghịch biến trên
- khoảng từ 1/2 đến dương vô cùng vậy ta
- chọn phương án c chính là phương án đúng
- cho ví dụ tiếp theo ví dụ thứ ba à
- a Cho hàm số FX có bảng xét dấu của SX
- như hình bên Câu hỏi đặt ra là hàm số GX
- bằng ép của x trừ 3 trừ x mũ 3 trên 3
- cộng với 2 x bình phương cộng 2019 đồng
- biến trên khoảng nào dưới đây và chúng
- ta có bún khoảng đây
- Thế thì để giải được bài này sẽ có một
- chút khó khăn hơn Tại vì cái hàm số GX
- người ta cho có một cái phần nửa sau
- kara phức tạp tự nhiên là cách làm của
- chúng ta cũng hoàn toàn tương tự với các
- câu trước bức đầu tiên ta tỉnh đạo hàm
- số GX vậy GX sẽ bằng đạo hàm của x trừ 3
- thì chín là một nhân gửi f phẩy x trừ 3
- - x bình phương cộng với 4x sau đó nhìn
- hơn bằng xét dấu của f7 thì ta thấy f
- phẩy x bằng 0 tại ba điểm x = -1 x bằng
- 1 hóa x = 3 vậy từ đây ta sinh ra là
- phẩy tại x trừ 3 bằng 0 khi và chỉ khi
- lại x - 3 = -1 x trừ 3 bằng một hoặc cờ
- bạc tương đương gửi Quảng 2x = 4x = 6
- tại bây giờ ta sẽ lập bảng xét dấu của
- gpx
- từ đầu tiên ra cỏ f phẩy x trừ 3 bằng 0
- tại ba nghiệm 2 4 và 6
- hãy Bây giờ nhìn lên dấu của SX ở cái
- bảng xét dấu của SX mà Đề đã cho thì ta
- sẽ liền được dấu của s phẩy x trừ 3
- tương tự đó là Dương âm dương và âm tiếp
- theo chúng ta sẽ điền dấu của đa thức
- chứa x bình phương cộng 4 x Thế thì đa
- thức này bằng 0 khi x bằng 0 hoặc lá x =
- 4 với x thuộc khoảng 4 đến dương vô cùng
- thì đa thức trừ x bình cộng 4 x sẽ mang
- dấu âm
- khoảng từ 0 đến 4 dương và từ âm vô cùng
- đến không mang nhiều âm
- vì
- vậy Cuối cùng chúng ta sẽ Điềm được dấu
- của gpx cho GV x = f phẩy x trừ 3 trừ x
- bình cộng 4 x chính là tổng của hai cái
- đang thích này trên khoảng từ âm vô cùng
- đến không hai đa thức này mang dấu âm vệ
- tổng của chúng cũng hoàng âm trên khoảng
- từ 0 đến 2 cách Vậy x trừ 3 mang đủ âm
- trừ x bình cộng 4 lại mang dấu dương
- Chúng Ta Chưa Kết luận được dấu của PX
- thì chúng ta để chống khuẩn khoảng thứ
- hai đến bốn Cả hai đều mang dấu dương
- thì dấu của gpx cũng là Dương
- ở trên khoảng từ 4 đến 6 số của cầu Vĩnh
- Tuy âm và trên khoảng giàu đến dương vô
- cùng chúng ta uống chung kết luận được
- dấu của gpx
- chị sẽ bây giờ nhìn lên bảng xét dấu của
- Cửu Vĩ thì ta nhận thấy
- hàm số GX sẽ đồng biến trên khoảng 2 đến
- 4 vì trên khoảng này gpx mang dầu dược
- Vậy chúng ta chọn phương án C bằng thứ 2
- đến 4 chính là đáp án của ví dụ 3
- và một ví dụ cuối cùng của dạng toán này
- ví dụ 4 Cho hàm số y bằng FX có đồ thị
- của hàm f phẩy x như hình ở dưới đây và
- các hỏi đặt ra làm số từ X = F của 5 -
- Hãy cộng 4 x bình trừ x đồng biến trên
- khoảng nào sau đây
- bước đầu tiên chúng ta tính đạo hàm của
- hàm số x r phẩy x thì bằng đạo hàm của 5
- - 2 x chỉ ra trừ 2 nhân gửi f phẩy của 5
- - 2 x + 8 x - 10 và giải ngừa phí bằng 0
- thì ta có em phải của 5 - 2x = 4 x trừ 5
- sau khi đó ta đặt t = 5 - 2 x
- Vì vậy một thì sẽ tương đương với ép
- phải tê thì bằng -2 t + năm sau đó chúng
- ta sẽ vẽ đồ thị hai hàm y = SC và y = -2
- t + năm trên cùng một hệ trục tọa độ thì
- ta sẽ tìm được kế hoành độ giao điểm
- hàm y = -2 t + năm là hàm số bậc nhất
- thì hệ để chúng ta có thể dễ dàng vẽ
- được đồ thị hàm số này rồi trên hình là
- cô đã vẽ ở đây Đây chỉ là đồ thị của hàm
- số y = -2 t + 5
- người ta nhận thấy ở đây có 3 do điểm
- Đây là một là hai Và đây là 3 vẽ cô ký
- hiệu hoành độ của ba do điểm này chính
- là Alpha 1
- A và Beta
- thế thì ta có
- T1 là bằng Alpha và gửi Alpha nhỏ thôi
- không T2 = 1 và T3 là bằng Beta và ta
- nhận thấy beta thì sẽ lớn hơn 5 phần 2
- từ giá trị của T thì ta được giá trị của
- xt1 thì tương ứng với x1t một nhỏ thu
- không
- ex1 sẽ phải lớn hơn 5/2 tích hay bằng
- một thể X2 = 2 và T3 lớn hơn 5 phần 2
- thì nghĩa là X3 nhỏ thua 5,4
- bây giờ chúng ta biểu diễn được các thí
- nghiệm x1 x2 3 trên trục số
- gọi X2 bằng hai ta ký hiệu X cả đây x 1
- lớn hơn 5/2 nghĩa là lớn hơn x 2 người
- ta ký hiệu tích một đây với X3 nhỏ thu
- 5/4 nghĩa là nhỏ hữu ích hay vậy ta sắp
- xếp được các nhiệm xai2 X1 theo thứ tự
- tăng dần từ trái qua phải và lúc nãy
- chúng ta đã tìm được giờ phải ích thì =
- -2 Nhân Kép phẩm của năm trừ 2x cộng 18
- X10 để yêu cầu hàm số x đồng biến trên
- khoảng nào cho nên chúng ta sẽ giải
- phương trình vừa phải x lớn hơn 0 điều
- này tương đương với f phẩy của 5 - 2 x
- thì nhỏ thua 4 x trừ 5 hay là ép phải
- của T thì nhỏ thua 2 T + năm với t là
- chúng ta đã đặt lúc nãy là bằng 5 - 2x
- Và bây giờ chúng ta quan sát đồ thị em
- gửi t thuộc khoảng từ Alpha đến một này
- vào khoảng từ beta đến dương vô cùng thi
- đô thị của hàm s phẩy t là cái đường màu
- xanh nằm dưới đồ thị hàm số y = -2 t +
- năm chính là đường màu đỏ nghĩa là trên
- các khoảng từ Alpha đến một và từ beta
- đến dương vô cùng thì sdt nhỏ thua 2T
- cộng 5 gửi t thuộc khoảng từ alpha này
- đến một này nghĩa là từ t1 đến t2 thì
- ích sẽ thuộc khoảng Tứ X2 đến X1 chính
- là thứ 2 đến x1 và T thực khoảng từ beta
- đến dương vô cùng
- beta chính đặt Ê ban
- Ừ thì tích sẽ không khoảng từ trừ vô
- cùng đến x3 với ta kết luận là hàm số GX
- bằng biến trên các khoảng thứ hai đến x1
- và thu âm cùng đến x3 với x1 lớn hơn 5
- phần 2 và X3 nhỏ thu 5/4 về nhìn lên các
- phương án thì ta nhận thấy phương án b
- là khoảng từ 2 đến 5/2 chính là phương
- án đúng vậy chúng ta kết thúc bài học
- ngày hôm nay ở đây cảm ơn các em đã chú
- ý lắng nghe và hẹn gặp lại các em trong
- các video bài giảng tiếp theo
OLMc◯2022


Bạn có thể đánh giá bài học này ở đây