Bài học cùng chủ đề
- Định lí Viète
- Giải phương trình bằng cách nhẩm nghiệm
- Tìm hai số khi biết tổng và tích
- Không giải phương trình, tính giá trị biểu thức nghiệm
- Giải phương trình bằng cách nhẩm nghiệm
- Tìm hai số khi biết tổng và tích
- Xét dấu các nghiệm của phương trình bậc hai
- Xác định điều kiện tham số để phương trình bậc hai thỏa mãn điều kiện cho trước
- Sự tương giao của hai đồ thị chứa tham số liên quan đến định lí Viète
- Phiếu bài tập tuần Định lí Viète
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Sự tương giao của hai đồ thị chứa tham số liên quan đến định lí Viète SVIP
Cho Parabol $(P): \, y=x^2$ và đường thẳng $d: \, y=2(m-1)x+2m+3.$
a) Tìm giá trị của $m$ để đường thẳng $d$ cắt trục tung tại điểm có tọa độ $(0;-5).$
b) Chứng minh rằng với mọi $m$ đường thẳng $d$ luôn cắt Parabol $(P)$ tại hai điểm phân biệt $A, \, B.$ Giả sử $A(x_A;y_A), \, B(x_B;y_B),$ tìm $m$ để $x_{A}^{2}+x_{B}^{2}=10.$
Hướng dẫn giải:
a) Vì đường thẳng $(d)$ cắt trục tung tại điểm có tọa độ $(0;-5)$ nên ta có:
$2m+3=-5 $
$2m=-8$
$m=-4$.
Vậy với $m=-4$ thì đường thẳng $(d)$ cắt trục tung tại tọa độ $(0;-5)$.
b) Phương trình hoành độ giao điểm của $d$ và $(P)$ là:
$x^2=2(m-1)x+2m+3$
$x^2-2(m-1)x-2m-3=0$ (*).
Ta có: $\Delta '=(m-1)^2+2m+3=m^2-2m+1+2m+3=m^2+4$.
Vì $m^2 \ge 0$ với mọi $m$ nên $\Delta '= m^2+4\ge 4>0$ với mọi $m$.
Vậy phương trình (*) có hai nghiệm phân biệt với mọi $m$
Suy ra đường thẳng $d$ luôn cắt $(P)$ tại hai điểm phân biệt với mọi $m$.
Theo định lí Viète ta có: $\left\{ \begin{aligned} & x_1+x_2=2(m-1) \\ & x_1x_2=-2m-3 \\ \end{aligned} \right.$
hay $\left\{ \begin{aligned} & x_A+x_B=2(m-1) \\ & x_Ax_B=-2m-3 \\ \end{aligned} \right.$
Mà $x_{A}^{2}+x_{B}^{2}=10$ nên
${{(x_A+x_B)}^{2}}-2x_Ax_B=10 $
$4{{(m-1)}^{2}}-2(-2m-3)=10 $
$4{{m}^{2}}-8m+4+4m+6=10$
$4{{m}^{2}}-4m=0$
$4m(m-1)=0$
$m=0$; $m=1$ (thỏa mãn điều kiện).
Vậy $m\in \left\{ 0;1 \right\}$.
Trong mặt phẳng tọa độ $Oxy,$ cho parabol $(P): \, y=x^2$ và đường thẳng $(d): \, y=2x+m^2$.
a) Chứng minh $(d)$ luôn cắt $(P)$ tại hai điểm phân biệt.
b) Tìm tất cả các giá trị của $m$ để $(d)$ cắt $(P)$ tại hai điểm phân biệt có hoành độ $x_1, \, x_2$ thỏa mãn $(x_1+1)(x_2+1)=-3$.
Hướng dẫn giải:
a) Xét phương trình hoành độ giao điểm của $(P)$ và $(d)$ là :
$x^2=2x+m^2$
$x^2-2x-m^2=0$ (*)
Ta có $\Delta '=(-1)^2-(-m)^2=m^2+1>0$ với mọi $m$
Nên phương trình (*) luôn có hai nghiệm phân biệt, do đó $(d)$ luôn cắt $(P)$ tại hai điểm phân biệt.
b) Vì $x_1; \, x_2$ là hoành độ giao điểm của $(d)$ và $(P)$ hay $x_1; \, x_2$ là nghiệm của phương trình (*).
Theo hệ thức Viète ta có: $x_1+x_2=2; \, x_1x_2=-m^2$.
Theo giả thiết: $ (x_1+1)(x_2+1)=-3 $
$ x_1x_2+x_1+x_2+1+3=0$
$ -m^2+2+1+3=0 $
$m^2=6 $
$m=\pm \sqrt{6}$.
Vậy $m=\pm \sqrt{6}$ là các giá trị cần tìm.
Cho hàm số $y=x^2$ và đường thẳng $(d): \, y=-x-m+1$ (với $m$ là tham số).
a) Vẽ parabol $(P)$ là đồ thị của hàm số $y=x^2$
b) Tìm tất cả các giá trị của tham số $m$ để $(d)$ cắt $(P)$ tại hai điểm phân biệt có hoành độ $x_1, \, x_2$ thỏa mãn $| x_1-x_2 |=2$.
Hướng dẫn giải:
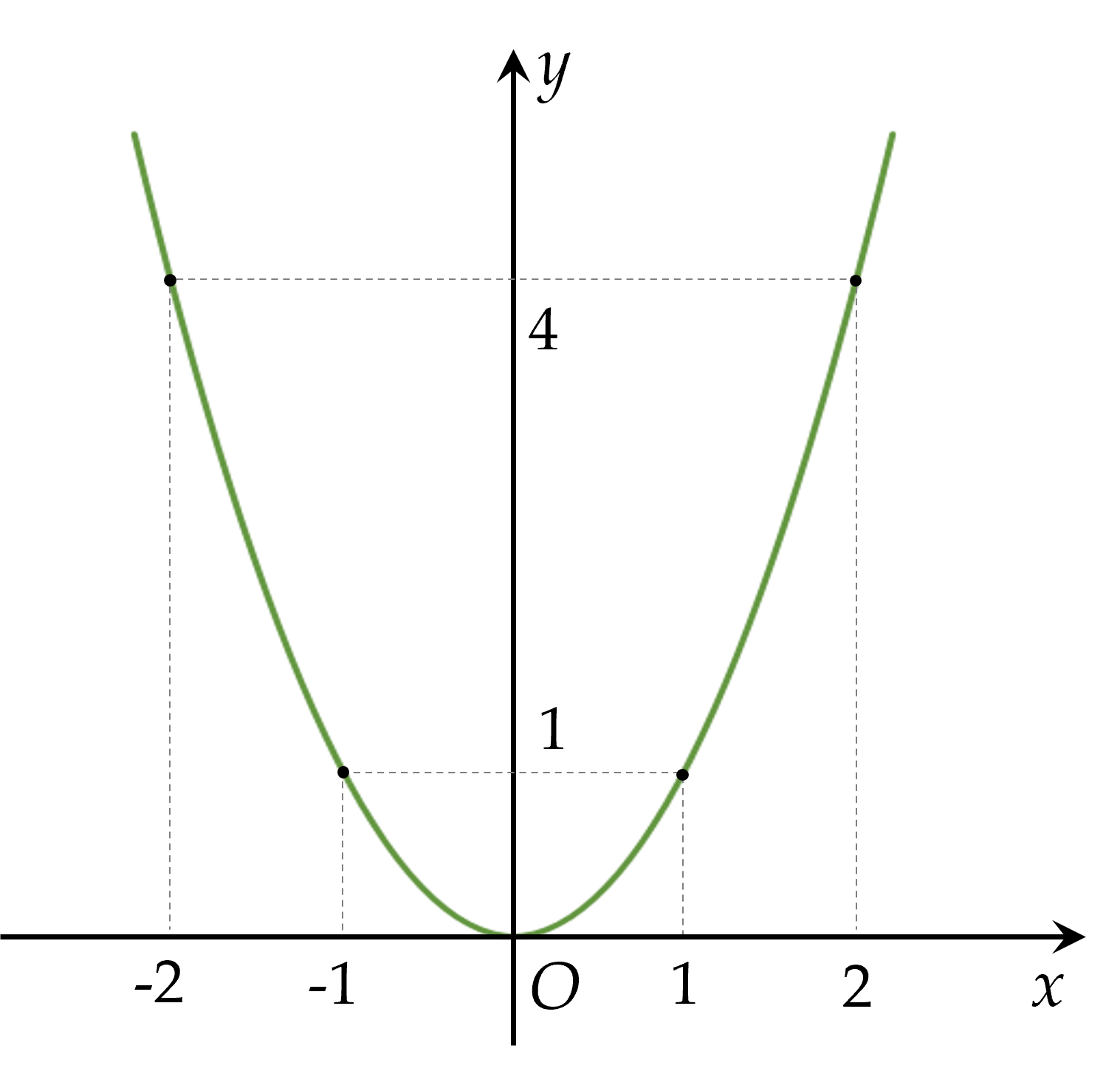
a) Vẽ parabol $(P)$ là đồ thị của hàm số $y=x^2$
- Bảng giá trị của $y$ tương ứng với giá trị của $x$ như sau:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y=x^2$ | $4$ | $1$ | $0$ | $1$ | $4$ |
- Vẽ các điểm $A( -2;4 ), \, B( -1;1 ), \, O( 0;0 ), \, C( 1;1 ), \, D( 2;4 )$ thuộc đồ thị hàm số $y=x^2$ trong mặt phẳng $Oxy$.
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số $y=x^2$.
b) Xét phương trình hoành độ giao điểm $x^2=-x-m+1$
$x^2+x+m-1=0$ (1)
Để phương trình (1) có hai nghiệm phân biệt thì $\Delta >0$
$1^2-4(m-1)>0$
$m<\dfrac{5}{4}$
Khi đó áp dụng hệ thức Viète: $x_1+x_2=-1; \, x_1x_2=m-1$.
Khi đó ta có: $\left| x_1-x_2 \right|=2 $
$( x_1-x_2 )^2=4$
$( x_1+x_2 )^2-4x_1x_2=4$
$1-4( m-1)=4 $
$m=\dfrac{1}{4}$ (tm)
Vậy $m=\dfrac{1}{4}$ là giá trị cần tìm.
Cho Parabol $(P): \, y=2x^2$ và đường thẳng $(d): \, y=-2x+m$ (với $m$ là tham số).
a) Vẽ Parabol $(P).$
b) Tìm tất cả các giá trị của tham số $m$ để $(d)$ cắt $(P)$ tại hai điểm phân biệt có hoành độ $x_1; \, x_2$ thỏa mãn $x_1+x_2-2x_1x_2=1$.
Hướng dẫn giải:
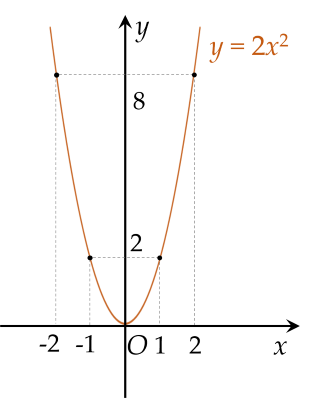
a) Vẽ Parabol $(P)$
Bảng giá trị của $y$ tương ứng với giá trị của $x$ như sau:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y=2x^2$ | $8$ | $2$ | $0$ | $2$ | $8$ |
Vẽ các điểm $A( -2;8 )$, $B( -1;2 )$, $O( 0;0 )$, $C( 1;2 )$, $D( 2;8 )$ thuộc đồ thị hàm số $y = 2x^2$ trong mặt phẳng $Oxy$.
Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số $y = 2x^2$.
b) Phương trình hoành độ giao điểm của $(d)$ và $(P)$ là:
$2x^2=-2x+m$
$2x^2+2x-m=0$ (1)
Ta có $\Delta' =1^2-2(-m)=1+2m$.
Để $(d)$ cắt $(P)$ tại hai điểm phân biệt khi
$\Delta' >0$
$1+2m>0$
$m>\dfrac{-1}{2} $
Với $m>\dfrac{-1}{2}$ thì $(d)$ cắt $(P)$ tại hai điểm phân biệt có hoành độ $x_1; \, x_2$.
Theo hệ thức Viète ta có: $x_1+x_2=-1; \, x_1x_2=\dfrac{-m}{2}$
Theo đề bài ta có: $x_1+x_2-2x_1x_2=1 $
$-1-2\dfrac{-m}{2}=1 $
$-1+m=1 $
$m=2$.
Vậy $m=2$ thì $(d)$ cắt $(P)$ tại hai điểm phân biệt có hoành độ $x_1; \, x_2$ thỏa mãn yêu cầu.
Trong mặt phẳng tọa độ $Oxy$, cho parabol $(P): \, y=x^2$ và đường thẳng $(d): \, y=mx+3$ ($m$ là tham số).
a) Vẽ parabol $(P)$.
b) Khi $m=2$, tìm tọa độ giao điểm của $(P)$ và $(d)$ bằng phép toán.
c) Tìm $m$ để đường thẳng $(d)$ và parabol $(P)$ luôn cắt nhau tại hai điểm phân biệt có hoành độ $x_1, \, x_2$ thỏa mãn $\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{3}{2}$.
Hướng dẫn giải:
a) Vẽ đồ thị hàm số $y=x^2$ $(P)$
- Bảng giá trị của $y$ tương ứng với giá trị của $x$ như sau:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y=x^2$ | $4$ | $1$ | $0$ | $1$ | $4$ |
- Vẽ các điểm $A( -2;4 ), \, B( -1;1 ), \, O( 0;0 ), \, C( 1;1 ), \, D( 2;4 )$ thuộc đồ thị hàm số $y=x^2$ trong mặt phẳng $Oxy$.
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số $y=x^2$.

b) Khi $m=2$ phương trình đường thẳng có dạng $(d): \, y=2x+3$.
Hoành độ giao điểm của $(P): \, y=x^2$ và $(d): \, y=2x+3$ là nghiệm của phương trình:
$x^2=2x+3$
$x^2-2x-3=0$
Vì $a-b+c=1-(-2)+(-3)=0$ nên phương trình có hai nghiệm $x_1=-1$; $x_2=-\dfrac{c}{a}=3$.
Với $x_1=-1$ thì $y_1=(-1)^2=1$.
Với $x_2=3$ thì $y_2=3^2=9$.
Vậy ta có hai giao điểm của $(P)$ và $(d)$ là $( -1;1 )$ và $( 3;9 )$.
c) Xét phương trình hoành độ giao điểm của $(P): \, y=x^2$ và $(d): \, y=mx+3$:
$x^2=mx+3 $
$x^2-mx-3=0 $ (1).
Để $(d)$ và $(P)$ luôn cắt nhau tại hai điểm phân biệt có hoành độ $x_1; \, x_2$ thì phương trình (1) phải luôn có hai nghiệm phân biệt $x_1; \, x_2$ thì $\Delta >0$
$(-m)^2-4.1.( -3)>0 $
$m^2+12>0$ (luôn đúng với mọi $m$)
Vậy với mọi $m$ thì phương trình (1) luôn có hai nghiệm phân biệt.
Theo hệ thức Viète, ta có: $\left\{ \begin{aligned} & x_1+x_2=m \\ & x_1.x_2=-3 \\ \end{aligned} \right.$.
Thay $x=0$ vào (1), ta có $0^2-m.0-3=-3 \ne 0$ với mọi $m$ nên (1) luôn có hai nghiệm phân biệt khác $0$ với mọi $m$.
Theo bài ra ta có: $\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{3}{2} $
$2x_2+2x_1=3x_1x_2$
$2( x_1+x_2 )=3x_1x_2$.
Thay hệ thức Viète, ta được: $2m=3.( -3 ) $
$2m=-9 $
$m=\dfrac{-9}{2}$.
Vậy $m=-\dfrac{9}{2}$ là giá trị cần tìm.
Cho hàm số $y=x^2$ có đồ thị $(P)$.
a) Vẽ đồ thị $(P)$ trên mặt phẳng tọa độ $Oxy$.
b) Tìm giá trị của $m$ để đường thẳng $(d)$: $y=2x-3m$ (với $m$ là tham số) cắt đồ thị $(P)$ tại hai điểm phân biệt có hoành độ là $x_1; \, x_2$ thỏa mãn điều kiện $x_1x_2^2-x_2(3m+2x_1)=12$.
Hướng dẫn giải:
a) Vẽ đồ thị $(P)$
- Bảng giá trị của $y$ tương ứng với giá trị của $x$ như sau:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y=x^2$ | $4$ | $1$ | $0$ | $1$ | $4$ |
- Vẽ các điểm $A( -2;4 ), \, B( -1;1 ), \, O( 0;0 ), \, C( 1;1 ), \, D( 2;4 )$ thuộc đồ thị hàm số $y=x^2$ trong mặt phẳng $Oxy$.
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số $y=x^2$.

b) Xét phương trình hoành độ giao điểm:
$x^2=2x-3m$
$x^2-2x+3m=0$ (*)
Để đường thẳng $(d)$: $y=2x-3m$ cắt đồ thị $(P)$ tại hai điểm phân biệt có hoành độ $x_1; \, x_2$ thì phương trình (*) phải có hai nghiệm $x_1; \, x_2$
$\Delta '=1-3m>0 $
$m<\dfrac{1}{3} $
Theo định lí Viète, ta có: $\left\{ \begin{aligned} & x_1+x_2=2 \\ &x_1x_2=3m \\ \end{aligned} \right.$
Vì $x_2$ là nghiệm của phương trình (*) nên
$x_{2}^{2}-2x_2+3m=0$
$3m=2x_2-x_{2}^{2} $
Suy ra $x_1x_{2}^{2}-x_2( 2x_2-x_{2}^{2}+2x_1)=12$
$x_1x_{2}^{2}+x_{2}^{3}-2x_2( x_1+x_2)=12$
$x_{2}^{2}( x_1+x_2)-2x_2( x_1+x_2)=12$
$(x_1+x_2)( x_{2}^{2}-2x_2)=12$
$2x_{2}^{2}-4x_2=12$
$x_{2}^{2}-2x_2=6 $
$-3m-6=0 $
$m=-2$ (tm)
Vậy $m=-2$ là giá trị cần tìm.
Trong mặt phẳng tọa độ $Oxy$, cho hàm số $y=\dfrac12x^2$ có đồ thị $(P)$ và đường thẳng $d$ có phương trình $y=x+\dfrac12m^2+m+1,$ với $m$ là tham số.
a) Vẽ đồ thị $(P)$.
b) Tìm $m$ để đường thẳng $d$ cắt $(P)$ tại hai điểm phân biệt có hoành độ $x_1; \, x_2$ sao cho $x_{1}^{3}+x_{2}^{3}=68$ .
Hướng dẫn giải:
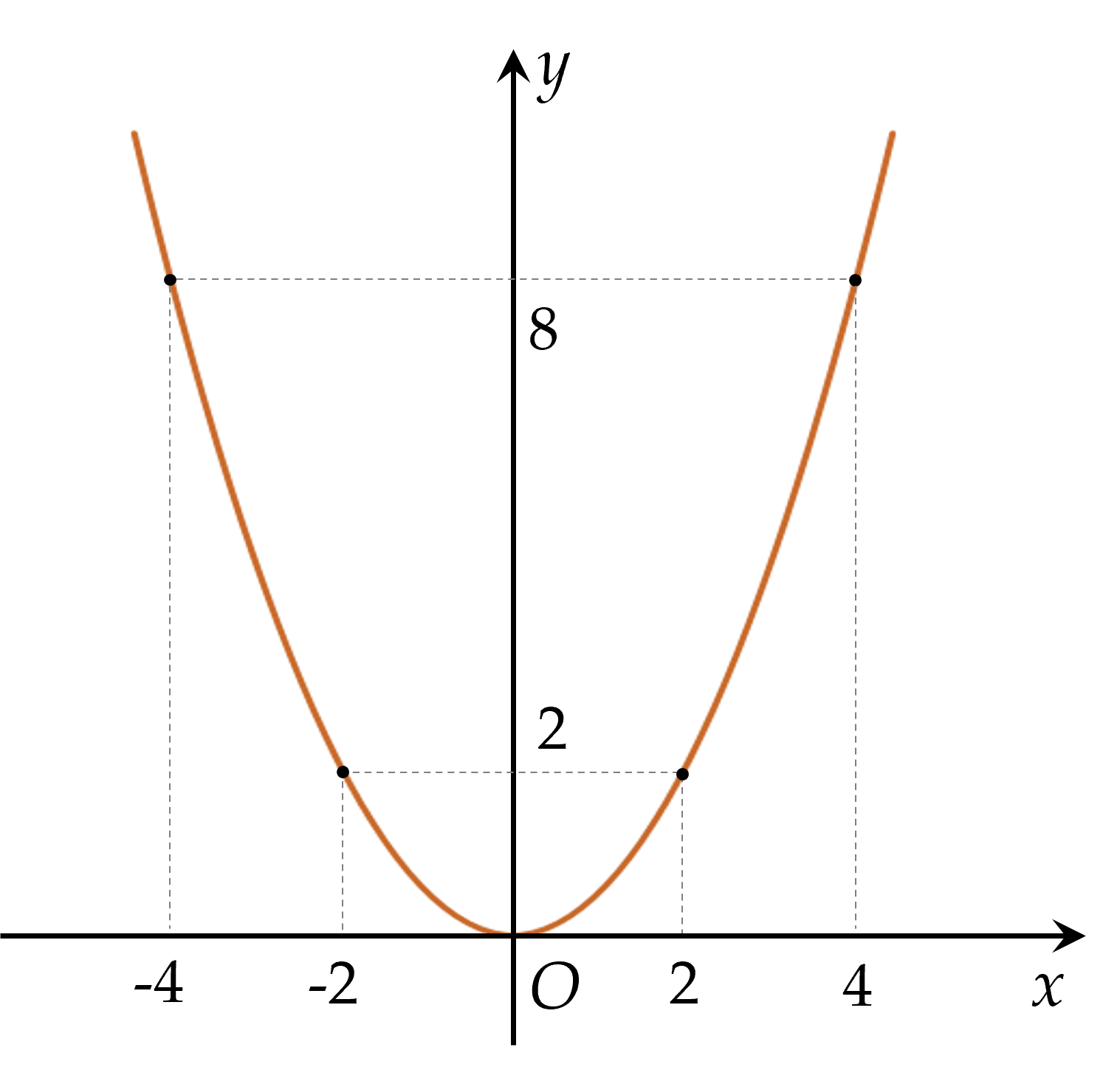
a) Vẽ đồ thị $(P)$.
- Bảng giá trị của $y$ tương ứng với giá trị của $x$ như sau:
| $x$ | $-4$ | $-2$ | $0$ | $2$ | $4$ |
| $y = \dfrac12x^2$ | $8$ | $2$ | $0$ | $2$ | $8$ |
- Vẽ các điểm $A( -4;8 ), \, B( -2;2 ), \, O( 0;0 ), \, C( 2;2 ), \, D( 4;8 )$ thuộc đồ thị hàm số $y=\dfrac12x^2$ trong mặt phẳng $Oxy$.
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số $y=\dfrac12x^2$.
b) Phương trình hoành độ giao điểm: $\dfrac12x^2=x+\dfrac12m^2+m+1$
$x^2-2x-m^2-2m-2=0$ (*)
Để đường thẳng $d$ cắt $(P)$ tại hai điểm phân biệt thì phương trình (*) có hai nghiệm phân biệt
$\Delta '>0$
$m^2+2m+3>0$
$(m+1)^2+2>0$
Do $(m+1)^2 \ge 0$ với mọi $m$ nên $(m+1)^2+2>0$ với mọi $m$.
Do đó phương trình (*) luôn có hai nghiệm phân biệt với mọi $m$
Suy ra đường thẳng $d$ luôn cắt $(P)$ tại hai điểm phân biệt có hoành độ $x_1; \, x_2$.
Khi đó áp dụng định lí Viète ta có: $x_1+x_2=2$; $x_1x_2=-m^2-2m-2$
Theo bài ra ta có: $x_1^3+x_2^3=68$
$(x_1+x_2)^3-3x_1x_2( x_1+x_2)=68$
$2^3-3( -m^2-2m-2 ).2=68$
$6m^2+12m-48=0$
$m^2+6m-8=0$ (**)
Vậy phương trình (**) có hai nghiệm phân biệt $m_1=2$; $m_2=-4.$
Cho hàm số $y=2x^2$ có đồ thị $(P)$.
a) Vẽ đồ thị $(P)$ trên mặt phẳng tọa độ $(Oxy)$.
b) Tìm tất cả các giá trị của tham số $m$ để đường thẳng $(d): \, y=2mx+1$ cắt $(P)$ tại hai điểm phân biệt có hoành độ $x_1; \, x_2$ thỏa mãn $x_1 < x_2$ và $\left| x_2 \right|-\left| x_1 \right|=2 \, 025$.
Hướng dẫn giải:
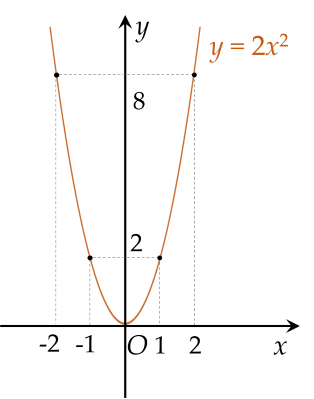
a) Vẽ đồ thị $(P)$.
Bảng giá trị của $y$ tương ứng với giá trị của $x$ như sau:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y=2x^2$ | $8$ | $2$ | $0$ | $2$ | $8$ |
Vẽ các điểm $A( -2;8 )$, $B( -1;2 )$, $O( 0;0 )$, $C( 1;2 )$, $D( 2;8 )$ thuộc đồ thị hàm số $y = 2x^2$ trong mặt phẳng $Oxy$.
Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số $y = 2x^2$.
b) Phương trình hoành độ giao điểm của $(P)$ và $(d)$ là
$ 2x^2=2mx+1$
$2x^2-2mx-1=0$ (1)
$\Delta '= (-m)^2-2.(-1)=m^2+2>0$ với mọi giá trị của $m$
Nên phương trình (1) luôn có hai nghiệm phân biệt với mọi giá trị của $m$.
Suy ra $(d)$ luôn cắt $(P)$ tại hai điểm phân biệt với mọi giá trị của $m$.
Theo định lí Viète ta có: $\left\{ \begin{aligned} & x_1+x_2=m \,\,\,(2) \\ & x_1x_2=-\dfrac{1}{2} \,\,\,(3) \\ \end{aligned} \right.$
Ta có $x_1<x_2$ mà $x_1x_2=\dfrac{-1}{2}<0$ suy ra $x_1<0<x_2$.
Khi đó $\left| x_2 \right|-\left| x_1 \right|=2 \, 025$
$x_2-(-x_1)=2\,025$
$x_2+x_1=2\,025$
$m=2\,025$.
