Tìm các số nguyên n để phân số D=n+11/2n-4 có giá trị là một số nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Để \(\dfrac{n+1}{n-2}\) có giá trị là một số nguyên thì n + 1 ⋮ n - 2
=> (n - 2) + 3 ⋮ n - 2
Vì (n - 2) ⋮ n - 2 nên 3 ⋮ n - 2
=> n - 2 ∈ Ư(3) ∈ {-3;-1;1;3}
=> n ∈ {-1;1;3;5}
b, Để \(\dfrac{4n+5}{2n-1}\) có giá trị là một số nguyên thì 4n + 5 ⋮ 2n - 1
=> (4n - 2) + 7 ⋮ 2n - 1
=> 2(2n - 1) + 7 ⋮ 2n - 1
Vì 2(2n - 1) ⋮ 2n -1 nên 7 ⋮ 2n - 1
=> 2n - 1 ∈ Ư(7) ∈ {-7;-1;1;7}
=> n ∈ {-3;0;1;4}

để 4/2n là số nguyên thi 4\(⋮\) 2n
=>2n\(\in\) Ư (4)
2n=1
n=1/2 loại
2n=2
n=2/2=1 chọn
2n=4
n=4/2=2 chọn

Để A là số nguyên thì 2n+8+2013 chia hết cho n+4
=>\(n+4\in\left\{\text{1;3;11;33;61;183;671;2013};-1;-3;-11;-33;-61;-183;-671;-2013\right\}\)
=>\(n\in\left\{-3;-1;7;29;57;179;667;2009;-5;-7;-15;-37;-65;-187;-675;-2017\right\}\)

a: Để A là phân số thì n-2<>0
=>n<>2
Khi n=-2 thì \(A=\dfrac{2\cdot\left(-2\right)+1}{-2-2}=\dfrac{-3}{-4}=\dfrac{3}{4}\)
b: Để A nguyên thì 2n+1 chia hết cho n-2
=>2n-4+5 chia hết cho n-2
=>\(n-2\in\left\{1;-1;5;-5\right\}\)
=>\(n\in\left\{3;1;7;-3\right\}\)

A=\(\frac{3n+9}{n-4}\)=\(\frac{3\left(n-4\right)+12+9}{n-4}=\frac{3\left(n-4\right)+21}{n-4}\)
Vì n-4 : hết cho n-4 => 3(n-4) chia hết cho n-4=> để A nguyên => 21 chia hết cho n-4
n-4 thuộc Ư(21)=> n-4 thuộc {-21;-7;-3;-1;1;3;7;21} =>n thuộc {-17;-3;1;3;5;7;25}

a. ĐK : \(n\ne-4\)
\(A=\frac{n+1}{n+4}=\frac{n+4-3}{n+4}=1-\frac{3}{n+4}\)
\(\Rightarrow n+4\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
| n + 4 | 1 | -1 | 3 | -3 |
| n | -3 | -5 | -1 | -7 |
b, ĐK : \(n\ne-1\)
\(B=\frac{3n-1}{n+1}=\frac{3\left(n+1\right)-4}{n+1}=3-\frac{4}{n+1}\)
\(\Rightarrow n+1\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
| n + 1 | 1 | -1 | 2 | -2 | 4 | -4 |
| n | 0 | -2 | 1 | -3 | 3 | -5 |
c,ĐK : \(n\ne\frac{1}{2}\)
\(C=\frac{6n+5}{2n-1}=\frac{3\left(2n-1\right)+8}{2n-1}=3+\frac{8}{2n-1}\)
\(\Rightarrow2n-1\inƯ\left(8\right)=\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
| 2n - 1 | 1 | -1 | 2 | -2 | 4 | -4 | 8 | -8 |
| n | 1 | 0 | 3/2(loại) | -1/2(loại) | 5/2(loại) | -3/2(loại) | 9/2(loại) | -7/2(loại) |

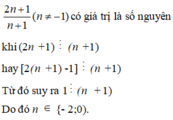
D nguyên <=> \(\frac{n+11}{2n-4}\) nguyên
<=> \(n+11⋮2n-4\)
=> \(2\left(n+11\right)⋮2n-4\)
=> \(2n+22⋮2n-4\)
=> \(\left(2n-4\right)+4+22⋮2n-4\)
=> \(\left(2n-4\right)+26⋮2n-4\)
\(2n-4⋮2n-4\)
=> \(26⋮2n-4\)
=> \(2n-4\inƯ\left(26\right)\)
đến đây dễ r`, bn tự lm tiếp đi !