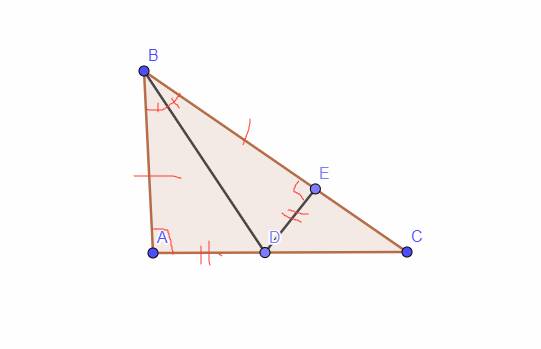
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = AB Tia phân giác góc B cắt A tại D
a, CM tam giác ABD = tam giác EBD
b, Tính số đo của góc BED
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 7 2023
a)Xet ΔABD va ΔEBD co:
AB=EB(GT)
∠ABD = ∠EBD(BD la tia phan giac ∠ABE)
BD chung
⇒ΔABD = ΔEBD(c.g.c)
b)theo cau a co :ΔABD = ΔEBD
⇒DA=DE(2 canh tuong ung)
c)theo cau a co:ΔABD = ΔEBD
⇒∠BAD=∠BED( 2 goc tuong ung)
Ma ∠BAD=90do
⇒∠BED = 90do
23 tháng 12 2023
a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
=>DA=DE
=>D nằm trên đường trung trực của AE(1)
ta có: BA=BE
=>B nằm trên trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE tại trung điểm của AE
c: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Ta có: AH\(\perp\)BC
DE\(\perp\)BC
Do đó: AH//DE
d: Ta có: \(\widehat{EDC}+\widehat{ACB}=90^0\)(ΔEDC vuông tại E)
\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{EDC}=\widehat{ABC}\)
e: Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAK=ΔDEC
=>AK=EC và DK=DC
Ta có: BA+AK=BK
BE+EC=BC
mà BA=BE và AK=EC
nên BK=BC
=>B nằm trên đường trung trực của KC(3)
Ta có: DK=DC
=>D nằm trên đường trung trực của KC(4)
Ta có: MK=MC
=>M nằm trên đường trung trực của KC(5)
Từ (3),(4),(5) suy ra B,D,M thẳng hàng
20 tháng 6 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
BA=BE
=>ΔBAD=ΔBED
b: Xét ΔBAE có BA=BE và góc B=60 độ
nên ΔBAE đều
=>BE=AB=6cm
=>BC=12cm
11 tháng 12 2021
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
11 tháng 12 2021
\(d,\) Gọi \(AE\cap BD=\left\{H\right\}\)
\(\left\{{}\begin{matrix}\widehat{ABH}=\widehat{EBH}\\AB=AE\\BH\text{ chung}\end{matrix}\right.\Rightarrow\Delta ABH=\Delta EBH\left(c.g.c\right)\\ \Rightarrow\widehat{BHA}=\widehat{BHE}\\ \text{Mà }\widehat{BHE}+\widehat{BHA}=180^0\left(\text{kề bù}\right)\\ \Rightarrow\widehat{BHE}=\widehat{BHA}=90^0\\ \Rightarrow BH\bot AE\\ \Rightarrow BD\bot AE\)
11 tháng 1 2022
a) Xét tam giác ABD và tam giác EBD:
+ AB = EB (gt).
+ BD chung.
+ \(\widehat{ABD}=\widehat{EBD}\) (BD là phân giác).
\(\Rightarrow\) Tam giác ABD = Tam giác EBD (c - g - c).
b) Tam giác ABD = Tam giác EBD (cmt).
\(\Rightarrow\) \(\widehat{BAD}=\widehat{BED}\) (2 góc tương ứng).
Mà \(\widehat{BAD}=90^o\) (Tam giác ABC vuông tại A).
\(\Rightarrow\) \(\widehat{BED}=90^o\)
c) Xét tam giác ABE: BA = BE (gt).
\(\Rightarrow\) Tam giác ABE cân tại B.
Mà BD là phân giác (gt).
\(\Rightarrow\) BD là đường cao (Tính chất tam giác cân).
\(\Rightarrow\) \(BD\perp AE.\)
6 tháng 3 2023
`a)`
Có `BD` là p/g của `hat(ABC)(GT)=>hat(B_1)=hat(B_2)`
Xét `Delta ABD` và `DElta EBD` có :
`{:(BA=BE(GT),(hat(B_1)=hat(B_2)(cmt),(BD-chung):}}`
`=>Delta ABD=Delta EBD(c.g.c)(đpcm)`
`b)`
Có `Delta ABD=Delta EBD(cmt)=>hat(A)=hat(E_1)` ( 2 góc t/ứng )
mà `hat(A)=90^0`
nên `hat(E_1)=90^0(đpcm)`
6 tháng 3 2023
`\color {blue} \text {_Namm_}`
`a,`
Xét Tam giác `ABD` và Tam giác `EBD` có:
`BA=BE (g``t)`
\(\widehat{ABD}=\widehat{EBD}\) `(` tia phân giác \(\widehat{ABE}\) `)`
`BD` chung
`=>` Tam giác `ABD =` Tam giác `EBD (c-g-c)`
`b,` Vì Tam giác `ABD =` Tam giác `EBD (a)`
`->`\(\widehat{BAD}=\widehat{BED}\) `(2` góc tương ứng `)`
Mà góc \(\widehat{A}\) vuông `(`\(\widehat{A}=90^0\) `)`
`-> `\(\widehat{BAD}=\widehat{BED}=90^0\)
`c,` Vì Tam giác `ABD =` Tam giác `EBD (a)`
`-> DE=DA (2` cạnh tương ứng `)`
Xét Tam giác `DEC:`
\(\widehat{DEC}=90^0\) `-> DC` là cạnh lớn nhất `-> DC>DE`
Mà `DE=DA -> DC>DA`
a)Xét tam giác ABD và tam giác EBD có:
AB=BE (gt)
\(\widehat{ABD}\)=\(\widehat{CBD}\)
BD là cạnh chung
Vậy \(\Delta ABD\)= \(\Delta EBD\)(c-g-c)
b) Vì \(\Delta ABD\)= \(\Delta EBD\)(cmt)
Nên \(\widehat{BAD}=\widehat{BED}\)= 90 độ
a , Xét tam giác ABD và tam giác EBD ta có :
cạnh BD chung
góc ABD= góc DBE [ BD là tia p/g của góc ABE ]
BA=BE [ gt ]
=> tam giác ABD = tam giác EBD [ c.g.c ]
b, Vì tam giác ABD= tam giác EBD [ cmt ]
=> góc A = góc EBD [ 2 góc tương ứng ]
Mà góc A = 90 độ
=> góc EBD = 90 độ
chúc bạn học tốt kết bạn với mình nha