b) Cho A= Tính A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có:
a = log 3 15 = log 3 ( 3 , 5 ) = log 3 3 + log 3 5 = 1 + log 3 5
Suy ra log 3 5 = a – 1
b = log 3 10 = log 3 ( 2 , 5 ) = log 3 2 + log 3 5
Suy ra log 3 2 = b − log 3 5 = b − (a − 1) = b – a + 1
Do đó:
log 3 50 = log 3 0 , 5 ( 2 . 52 ) = 2 log 3 2 + 4 log 3 5 = 2 (b – a + 1) + 4(a − 1) = 2a + 2b − 2
b) Ta có:
log 140 63 = log 140 ( 32 . 7 ) = 2 log 140 3 + log 140 7
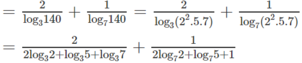
Từ đề bài suy ra:
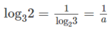
log 0 , 5 π . log 7 5 = log 7 2 . log 2 3 . log 35 = cab
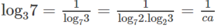
Vậy
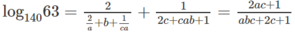

a) ta có: A = 2156 + 357
=> A - 357 = 2156 + (357-357)
A - 357 = 2156
=> A - 2156 = (2156-2156) + 357
A - 2156 = 357
b) ta có: B = 9475 - 7436
=> B + 7436 = 9475 - (7436-7436)
B + 7236 = 9475
=> 9475 - B = 9475 + 9475 - 7436
9475 -B = 2.9475 - 7436
( phần b câu 2 hình như bn chép sai)

Ta có :
M = 2( a3 + b3 ) - 3( a2 + b2 )
= 2( a + b ) ( a2 - ab + b2 ) - 3( a2 + b2 )
= 2( a2 - ab + b2 ) - 3 ( a2 + b2 )
= 2a2 - 2ab + 2b2 - 3a2 - 3b2
= -a2 - 2ab - b2
= - ( a + b )2
= -1


a)A - 357 = 2156 và A - 2156 = 357
b)B + 7436 = 9475 và 9475 - B = 7436


\(a,\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0=>\frac{ab+bc+ac}{abc}=0=>ab+bc+ac=0.abc=0\)
Mà \(a+b+c=1=>\left(a+b+c\right)^2=1=>a^2+b^2+c^2+2ab+2bc+2ac=1\)
\(=>a^2+b^2+c^2+2\left(ab+bc+ac\right)=1=>a^2+b^2+c^2=1-0=1\) (vì ab+bc+ac=0)
\(b,S=\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}=\left(\frac{a}{b+c}+1\right)+\left(\frac{b}{a+c}+1\right)+\left(\frac{c}{a+b}+1\right)-3\)
\(=\frac{a+b+c}{b+c}+\frac{a+b+c}{a+c}+\frac{a+b+c}{a+b}-3=\left(a+b+c\right).\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c}\right)-3\)
\(=2014.\frac{1}{2014}-3=1-3=-2\)
Vậy.....................