Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
MNPQ là hình thoi vì là hình bình hành có hai cạnh kề bằng nhau.
Ta có MN song song và bằng QP (vì cùng song song với AC và bằng 1/2 của AC theo tính chất đường trung bình của tam giác)
Vậy MNPQ là hình bình hành vì có 2 canh đối song song và bằng nhau.
mk chi lam dc y a thui
http://lazi.vn/edu/exercise/cho-tu-giac-abcd-goi-m-n-p-q-lan-luot-la-trung-diem-cua-cac-canh-ab-cd-ad-bc-chung-minh-vecto-mp-qn-mq-pn . Bạn vào link này nhé
Sửa đề: M,N,P,Q lần lượt là trung điểm của AB,BC,CD,DA
a: AB//DC
\(P\in DC\)
Do đó: AB//DP
AB=DC/2
DP=DC/2=PC
Do đó: AB=DP=CP
Xét tứ giác ABPD có
AB//PD
AB=PD
Do đó: ABPD là hình bình hành
b: Xét ΔABC có
M,N lần lượt là trung điểm của BA,BC
=>MN là đường trung bình của ΔBAC
=>MN//AC và MN=AC/2(1)
Xét ΔADC có
Q,P lần lượt là trung điểm của DA,DC
=>QP là đường trung bình
=>QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
Xét tứ giác MNPQ có
MN//PQ
MN=PQ
Do đó: MNPQ là hình bình hành
c: ABPD là hình bình hành
=>AP cắt BD tại trung điểm của mỗi đường
=>E là trung điểm của AP và BD
Xét ΔADP có
Q,E lần lượt là trung điểm của AD,AP
=>QE là đường trung bình
=>QE//DP
=>QE//DC
Xét ΔBDC có
E,N lần lượt là trung điểm của BD,BC
=>EN là đường trung bình
=>EN//DC
EN//DC
QE//DC
mà QE và EN có điểm chung là E
nên Q,E,N thẳng hàng
xét tam giác ADC có Q là trung điểm của AD(gt)
P là trung điểm của DC (gt)
=> QP là đường trung bình của tam giác ADC
=> QP=AC/2, QP// AC (1)
xét tam giác ABC có M là trung điểm của AB (gt)
N là trung điểm của BC (gt)
=> NM là đường trung bình của tam giác ABC
=> NM = AC/2, NM // AC (2)
từ (1) và (2) => NM = QP, NM // QP => MNPQ là HBH(vì là tứ giác có 2 cạnh đối vừa // vừa = nhau)
b) ABCD là Hthang cân => \(\widehat{BAD}=\widehat{ABC}\), AD = BC (t/c Hthang cân)
AD = BC => AQ = BN
xét tam giác AQM và tam giác MBN
có AM=MB (gt)
\(\widehat{QAM}=\widehat{MBN}\)(cmt)
AQ = BN (cmt)
=> tam giác AQM = tam giác BNM(c-g-c)
=> QM=MN (2 cạnh tương ứng)
HBH MNPQ có QM = MN (cmt)
=> MNPQ là Hthoi (vì là HB có 2 cạnh kề = nhau)
MP là đường chéo => MP là tia phân giác của \(\widehat{QMN}\)(t/c Hthoi)
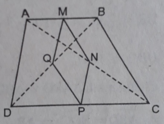
Tam giác BCD có :
BN = NC ( gt )
DP = PC ( gt )
\(\Rightarrow\)NP là đường trung bình tam giác BCD ( 1 )
Tam giác ADB có :
AQ = QD ( gt )
AM = MB ( gt )
\(\Rightarrow\)QM là đường trung bình tam giác ADB ( 2 )
Từ ( 1 ) , ( 2 ) suy ra NP = QM , NP // QM
\(\Rightarrow\)MNEF là hình bình hành ( đến đây bạn tự chứng minh tiếp hình thoi )
c) Để MNPQ là hình vuông thì ta chứng minh ABCD là hình thang cân có 2 đường chéo vuông góc với nhau