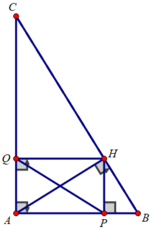
Cho tam giác ABC vuông tại A có AB = 30 cm, BC = 50 cm. Kẻ đường cao AH. Gọi P và Q lần lượt là hình chiếu H trên AB và AC.
a. Tính độ dài BH, CH.
b. Tính độ dài AH.
c. Tính số đo góc B và góc C.
d. Tính độ dài PQ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 1 2018
a, Áp dụng hệ thức giữa cạnh và đường cao trong các tam giác vuông
∆AHC và ∆AHB ta có:
AE.AC = A H 2 = AD.AB => ∆AHC ~ ∆AHB(c.g.c)
b. Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ∆ABC tính được AH = 3cm => DE = 3cm
Trong ∆AHB vuông ta có:
tan A B C ^ = A H H B => A B C ^ ≈ 56 0 , S A D E = 27 13 c m 2
3 tháng 12 2021
\(a,AC=\sqrt{BC^2-AB^2}=3\sqrt{3}\left(cm\right)\\ \sin B=\dfrac{AC}{BC}=\dfrac{\sqrt{3}}{2}=\sin60^0\\ \Rightarrow\widehat{B}=60^0\\ \Rightarrow\widehat{C}=30^0\)
29 tháng 10 2023
a: BC=BH+CH
=3,6+6,4=10(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=3,6\cdot6,4=23,04\)
=>\(AH=\sqrt{23,04}=4,8\left(cm\right)\)
ΔAHC vuông tại H
=>\(AC^2=AH^2+HC^2\)
=>\(AC^2=4,8^2+6,4^2=64\)
=>AC=8(cm)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}\simeq53^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}\simeq90^0-53^0=37^0\)
b: Sửa đề; \(AM\cdot MB+AN\cdot NC=MN^2\)
Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
=>AMHN là hình chữ nhật
Xét ΔHAB vuông tại H có HM là đường cao
nên \(AM\cdot MB=HM^2\)
Xét ΔHAC vuông tại H có HN là đường cao
nên \(AN\cdot NC=HN^2\)
\(AM\cdot MB+AN\cdot NC=HM^2+HN^2=MN^2\)
c: AK\(\perp\)MN
=>\(\widehat{ANM}+\widehat{KAC}=90^0\)
mà \(\widehat{ANM}=\widehat{AHM}\)(AMHN là hình chữ nhật)
nên \(\widehat{AHM}+\widehat{KAC}=90^0\)
mà \(\widehat{AHM}=\widehat{B}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{B}+\widehat{KAC}=90^0\)
mà \(\widehat{B}+\widehat{KCA}=90^0\)
nên \(\widehat{KAC}=\widehat{KCA}\)
=>KA=KC
\(\widehat{KAC}+\widehat{KAB}=90^0\)
\(\widehat{KCA}+\widehat{KBA}=90^0\)
mà \(\widehat{KAC}=\widehat{KCA}\)
nên \(\widehat{KAB}=\widehat{KBA}\)
=>KA=KB
mà KA=KC
nên KB=KC
=>K là trung điểm của BC
15 tháng 10 2021
b: Xét ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
hay \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét ΔADE vuông tại A và ΔACB vuông tại A có
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Do đó: ΔADE\(\sim\)ΔACB
Suy ra: \(\widehat{ADE}=\widehat{ACB}\)
21 tháng 10 2017
P/s : Bà chị có on thì tham khảo nhé "bí mật mong manh "
a/Áp dụng hệ thức lượng trong tam giác ta có:
HB=AB^2/BC=30^2:50=18cm
HC=BC-HB=50-18=32cm.
b/Ta có AH^2=HB.HC=18.32=576
-->AH=24cm
c/ Ta có sin B=AH/AB=24/30=4/5
=> góc B=53*
Góc C=90*-53*=37*
c)
Tg ABC (A=90)
SinB=AC/BC=4/5
=>B sấp xỉ 53^0
B+c=90
=>C=90-53 sấp xỉ 37 độ
d)
Xét tg APHQ
Có A=90(tg ABC vuông tại A)
P=90(HP vuông AB)
Q=90(HQ vuông góc AC
=> APHQ là hcn(dhnb)
=>AH=PQ=24(t/c hcn)
CM
7 tháng 11 2018
a) Xét tam giác ABC vuông tại A có:
A B 2 + A C 2 = B C 2
Tam giác ABC vuông tại A có AH là đường cao nên ta có:
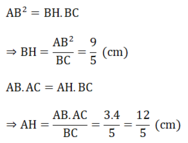
Ta có:
BH + CH = BC ⇒ CH = BC - BH = 5 - 9/5 = 16/5 (cm)
6 tháng 11 2021
a, \(BC=BH+HC=10\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}AH=\sqrt{BH\cdot HC}=4,8\left(cm\right)\\AB=\sqrt{BH\cdot BC}=6\left(cm\right)\end{matrix}\right.\)
\(\sin HCA=\dfrac{AB}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{HCA}\approx37^0\)