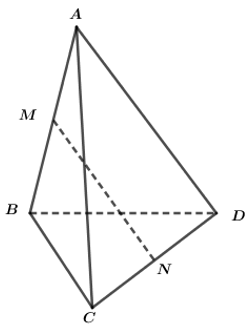
M và N lần lượt là trung điểm của BC ,CD của tứ giác ABCD.Chứng minh \(S\left(ABCD\right)\le\frac{1}{2}\left(AM+AN\right)^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 9 2021
Trên tia đối của PB lấy H sao cho BP = PH
ΔBPC và ΔHPD có:
BP = HP (cách vẽ)
\(\widehat{BPC}=\widehat{HPD}\left(đối.đỉnh\right)\) (đối đỉnh)
PC = PD (gt)
Do đó, ΔBPC=ΔHPD(c.g.c)
=> BC = DH (2 cạnh t/ứng)
và \(\widehat{PBC}=\widehat{PHD}\) (2 góc t/ứ), mà 2 góc này ở vị trí so le trong nên BC // HD
ΔABH có: M là trung điểm của AB (gt)
P là trung điểm của BH (vì HP = BP)
Do đó MP là đường trung bình của ΔABH
\(\Rightarrow MP=\dfrac{1}{2}AH\) ; MP // AH
\(\Rightarrow2MP=AH\)
Có: \(AD+DH\ge AH\) (quan hệ giữa 3 điểm bất kì)
\(\Leftrightarrow AD+BC\ge2MP\) (thay \(DH=BC;AH=2MP\))
\(\Leftrightarrow\dfrac{AD+BC}{2}\ge MP\)
Mà theo đề bài: \(MP=\dfrac{BC+AD}{2}\)
Do đó, \(AD+DH=AH\)
=> A,D,H thẳng hàng
Mà HD // BC (cmt) nên AD // BC
Tương tự: AB // CD
Tứ giác ABCD có: AD // BC (cmt);AB // CD (cmt)
Do đó, ABCD là hình bình hành
HQ
Hà Quang Minh
Giáo viên
11 tháng 1
a) Vì M và P lần lượt là trung điểm của hai cạnh AD, AC nên MP là đường trung bình của tam giác ADC.
\( \Rightarrow MP\parallel AB\parallel CD\,\,\left( 1 \right)\)
Vì P và N lần lượt là trung điểm của hai cạnh AC, BC nên PN là đường trung bình của tam giác ABC.
\( \Rightarrow PN\parallel AB\parallel CD\,\,\left( 2 \right)\)
Từ (1) và (2) ta có \(MP \equiv PN\) hay ba điểm M, N, P thẳng hàng.
b) Vì MP là đường trung bình của tam giác ADC nên \(MP = \frac{1}{2}DC\).
Vì PN là đường trung bình của tam giác ABC nên \(PN = \frac{1}{2}AB\).
Ta có:
\(MN = MP + PN = \frac{1}{2}DC + \frac{1}{2}AB = \frac{1}{2}\left( {DC + AB} \right)\)
Vậy \(MN = \frac{1}{2}\left( {AB + CD} \right)\).
con lợn và con chó nặng 102kg,con lợn và con bò nặng 231kg ,con chó và con bò nặng 177 kg .Trung bình mỗi con nặng bao nhiêu kg?
Ta có: Sabm = Samc ( chung đường cao, đáy bằng nhau)
Sadn = Sanc (chung đường cao, đáy bằng nhau)
=> Sabcd = 2Samcn
Mặt khác: Samn > Smnc => Samcn < 2Samn
Samn = 1/2(AM.AN. SinA) < 1/2(AM.AN) <= 1/2 . (AM + NA)^2/4 = (Am+AN)^2 / 8 (cô si)
=> Sabcd < 4. (am+an)^2 / 8 = 1/2 (am+an)^2