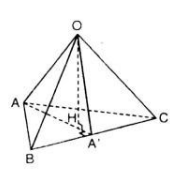
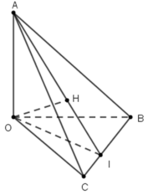
Cho tứ diện OABC có OA, OB , OC đôi một vuông góc với nhau a, CM: OA vuông góc với (OBC) b, gọi OK,OH lần lượt là đường cao của ∆OBC và ∆OAK. CM : OH vuông góc với (ABC) c, H là trực tâm của ∆ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 8 2023
tham khảo:
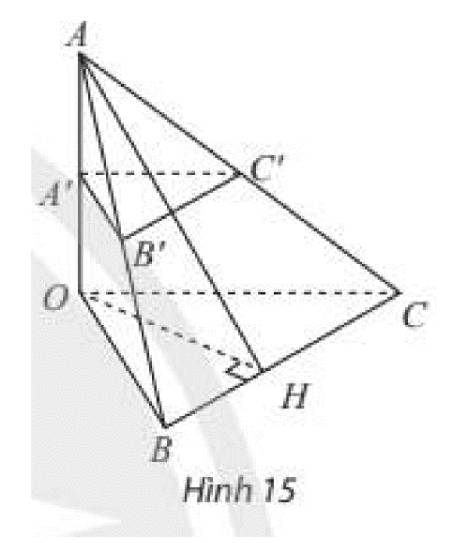
a) Tam giác AOB có A'B' là đường trung bình nên A'B'//AB hay A'B'//(OBC)
Tam giác AOC có A'C' là đường trung bình nên A'C"//AC hay A'C'//(OBC)
Suy ra (A'B'C')//(OBC)
Mà OA⊥(OBC) nên OA⊥(A′B′C′)
b) Vì OA⊥(OBC);BC∈(OBC) nên OA⊥CB
Ta có đường thẳng BC vuông góc với hai đường thẳng OH và OA cắt nhau cùng thuộc (AOH) nên BC⊥(OAH)
Mà tam giác ABC có B'C' là đường trung bình nên B'C'//BC
Suy ra B′C′⊥(AOH)
CM
6 tháng 10 2017
Đáp án A
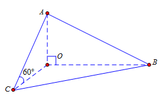
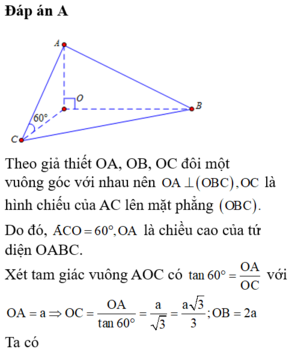
Theo giả thiết OA, OB, OC đôi một vuông góc với nhau nên O A ⊥ O B C , O C là hình chiếu của AC lên mặt phẳng O B C . Do đó, A C O ^ = 60 ° , O A là chiều cao của tứ diện OABC. Xét tam giác vuông AOC có tan 60 ° = O A O C với O A = a ⇒ O C = O A tan 60 ° = a 3 = a 3 3 ; O B = 2 a
Ta có S O B C = 1 2 O B . O C = 1 2 2 a . a 3 3 ; V O A B C = 1 3 O A . S O B C = 1 3 a . a 2 3 3 = a 3 3 9
CM
24 tháng 9 2017
Đáp án D
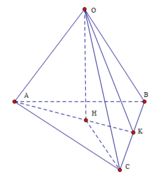
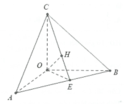
Đáp án A đúng vì Δ O A K , Δ O B C là các tam giác vuông
⇒ 1 O H 2 = 1 O A 2 + 1 O K 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
Đáp án B đúng vì B C ⊥ O A H , C A ⊥ O B H , A B ⊥ O C H ⇒ A H , B H , C H là các đường cao trong tam giác
Đáp án C đúng vì B C ⊥ O A H
Đáp án D sai vì nếu A H ⊥ O B C ⇒ A H ⊥ O K ⇒ mâu thuẫn
CM
6 tháng 3 2018
Đáp án A
*) Vì OA,OB,OC đôi một vuông góc với nhau nên
*)
theo trên B C ⊥ O A ⇒ B C ⊥ A H (2).
Từ (1) và (2) H là trực tâm tam giác ABC
*) Kẻ O I ⊥ B C tại I; O H ⊥ A I tại H
⇒ O H ⊥ ( A B C )
Ta có trong tam giác vuông OAC vuông tại O và OBC vuông tại O:
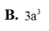
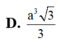
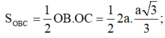
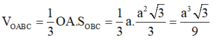
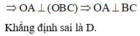
a: OA\(\perp\)OB
OA\(\perp\)OC
OB,OC cùng thuộc mp(OBC)
Do đó: OA\(\perp\)(OBC)
b: Ta có: BC\(\perp\)AK
BC\(\perp\)AO
AK,AO cùng thuộc mp(AKO)
Do đó: BC\(\perp\)(AKO)
=>BC\(\perp\)OH
Ta có: OH\(\perp\)BC
OH\(\perp\)AK
AK,BC cùng thuộc mp(ABC)
Do đó: OH\(\perp\)(ABC)