Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

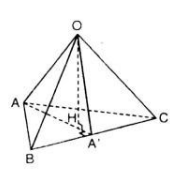
a: OA\(\perp\)OB
OA\(\perp\)OC
OB,OC cùng thuộc mp(OBC)
Do đó: OA\(\perp\)(OBC)
b: Ta có: BC\(\perp\)AK
BC\(\perp\)AO
AK,AO cùng thuộc mp(AKO)
Do đó: BC\(\perp\)(AKO)
=>BC\(\perp\)OH
Ta có: OH\(\perp\)BC
OH\(\perp\)AK
AK,BC cùng thuộc mp(ABC)
Do đó: OH\(\perp\)(ABC)

Cau 33:
\(\left|\overrightarrow{u}-\overrightarrow{v}\right|=\sqrt{\left(\overrightarrow{u}-\overrightarrow{v}\right)^2}=\sqrt{u^2+v^2-2\cdot u\cdot v\cdot cos120}\)
\(=\sqrt{4^2+3^2-2\cdot4\cdot3\cdot\dfrac{-1}{2}}=\sqrt{37}\)

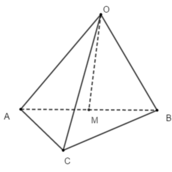
Tam giác OAB vuông tại O (OA ⊥ OB)
Theo định lý Py-ta-go ta có: A B = O A 2 + O B 2 = 1 2 + 1 2 = 2
Tương tự BC = 2
Ta có: OM là trung tuyến của tam giác OAB vuông tại O
Nên OM = 1/2AB = 1 2 . 2 = 2 2
Đáp án D

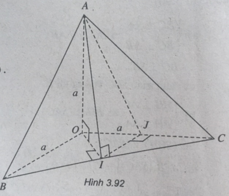
a) (BC ⊥ OA & BC ⊥ OI ⇒ BC ⊥ (OAI)
⇒ (ABC) ⊥ (OAI).
b) + Xác định góc α giữa AB và mặt phẳng (AOI)
(A ∈ (OAI) & BI ⊥ (OAI) ⇒ ∠[(AB,(OAI))] = ∠(BAI) = α.
+ Tính α:
Trong tam giác vuông BAI, ta có: sinα = 1/2 ⇒ α = 30o.
c) Xác định góc β giữa hai đường thẳng AI và OB:
Gọi J là trung điểm OC,
ta có: IJ // OB và IJ ⊥ (AOC). Như vậy:
∠[(AB,OB)] = ∠[(AI,IJ)] = ∠(AIJ) = β.
+ Tính góc:
Trong tam giác IJA,
ta có: tan β = AJ/IJ = √5 ⇒ β = arctan√5.