Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. So sánh ∠(BAM) và ∠(MAC).
Ko cần vẽ thêm 1 cạnh ...
Đọc tiếp
Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. So sánh ∠(BAM) và ∠(MAC).
Ko cần vẽ thêm 1 cạnh nữa
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
25 tháng 10 2018
Trên tia đối tia MA lấy điểm D sao cho MD = MA
Xét ΔAMB và ΔDMC, ta có:
MA = MD (theo cách vẽ)
∠(AMB) = ∠(DMC) (đối đỉnh)
MB = MC (gt)
Suy ra: ΔAMB = ΔDMC (c.g.c)
Suy ra: AB = CD (2 cạnh tương ứng)
và ∠D = ∠A1(2 góc tương ứng) (1)
Mà AB < AC (gt)
nên: CD < AC
Trong ΔADC, ta có: CD < AC
Suy ra: ∠D > ∠A2(đối diện cạnh lớn hơn là góc lớn hơn) (2)
Từ (1) và (2) suy ra: ∠A1 > ∠A2hay ∠(BAM) > ∠(MAC) .
KS
1
PN
17 tháng 3 2016
Trên tia \(AM\) của tam giác \(ABC\) lấy điểm \(I\) sao cho \(AM=IM\)
Ta có: \(AM=IM\) (theo giả thiết)
góc \(M_1\) \(=\) góc \(M_2\) (đối đỉnh)
\(MC=MB\) (do \(M\) là trung điểm của \(BC\))
nên \(\Delta AMC=\Delta IMB\) \(\left(cgc\right)\)
suy ra góc \(MAC\) \(=\) góc \(MIB\) (hai góc tương ứng)
Do đó, \(BI=AC>AB\)
Khi đó, xét \(\Delta ABI\) có \(BI>AB\)
nên góc \(BAI\) \(>\) góc \(BIA\)
\(\Leftrightarrow\) góc \(BAM\) \(>\) góc \(MAC\)
CM
4 tháng 6 2019
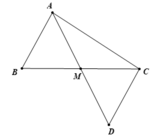
c. Trong tam giác ADC có CD < AC ⇒ ∠(DAC) < ∠(ADC) (1 điểm)
Mà ∠(BAM) = ∠(ADC) ( 2 góc tương ứng vì ΔABM = ΔDCM) (0.5 điểm)
Suy ra ∠(MAB) > ∠(MAC) (0.5 điểm)
NN
1
JT
6 tháng 3 2018
* Xét ΔABM và ΔMCE: AM=ME
\(\widehat{AMB}=\widehat{CME}\)
BM=MC
⇒ ΔABM = ΔMCE (c.g.c)
⇒ CE=AB ( 2 cạnh tương ứng)
⇒ \(\widehat{BAM}=\widehat{CEM}\)( 2 góc tương ứng)
Vì AB<AC
⇒ CE<AC
Xét ΔACE có: CE< AC
⇒ \(\widehat{MAC}= \widehat{CEM}\)
mà \(\widehat{BAM}=\widehat{CEM}\) (cmtrn)
⇒ \(\widehat{BAM}=\widehat{MAC}\) (đpcm)
TN
0
28 tháng 2 2022
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{4}=\dfrac{AC}{5}=\dfrac{BC}{6}=\dfrac{AB+AC+BC}{4+5+6}=\dfrac{30}{15}=2\)
Do đó: AB=8cm; AC=10cm; BC=12cm
=>\(\widehat{C}< \widehat{B}< \widehat{A}\)
b: \(\cos MAB=\dfrac{AB^2+AM^2-BM^2}{2\cdot AB\cdot AM}=\dfrac{AB^2+AM^2-CM^2}{2\cdot AB\cdot AM}\)
\(\cos MAC=\dfrac{AM^2+AC^2-MC^2}{2\cdot AM\cdot AC}\)
mà \(\dfrac{AB^2+AM^2-MC^2}{2\cdot AM\cdot AC}< \dfrac{AM^2+AC^2-MC^2}{2\cdot AM\cdot AC}\)
nên \(\widehat{MAB}>\widehat{MAC}\)
khó thế
có