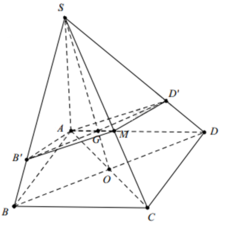
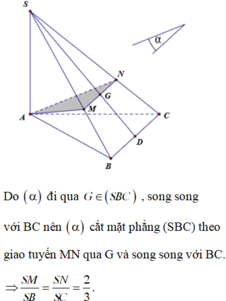
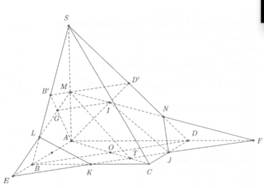
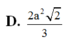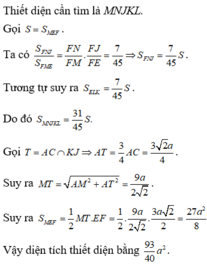Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a, tâm O, SA = SB = 4a. Gọi G là trọng tâm tam giác BCD, (α) là mặt phẳng qua G và song song với (SAD). Tính diện tích thiết diện của (α) và hình chóp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
3 tháng 12 2021
Qua G kẻ đường thẳng d song song với AB.
\(H=d\cap SB;K=d\cap SA\)
Kẻ KP//AD, HT//BC \(\left(P\in SD;T\in SC\right)\)
\(\Rightarrow KHTP\) là thiết diện cần tìm.
\(\dfrac{HK}{AB}=\dfrac{HT}{BC}=\dfrac{KP}{AD}=\dfrac{PT}{CD}=\dfrac{2}{3}\)
Mà \(AB=BC=CD=DA\Rightarrow KH=HT=TP=PK\)
\(\Rightarrow KHPT\) là hình vuông.
CM
27 tháng 8 2019
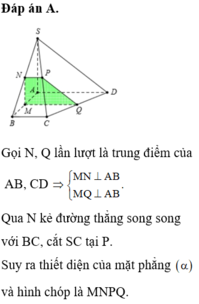
Đáp án D
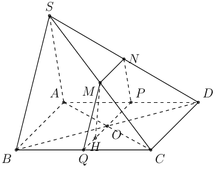
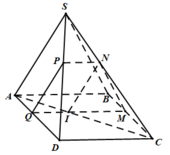
Qua O dựng đường thẳng P Q ∥ A B . Vậy P, Q lần lượt là trung điểm của AD và BC.
Qua P dựng đường thẳng P N ∥ S A . Vậy N là trung điểm của SD
Qua Q dựng đường thẳng Q M ∥ S B . Vậy M là trung điểm của SC.
Nối M và N ⇒ thiết diện của (P) và hình chóp S.ABCD là tứ giác MNPQ.
Vì P Q ∥ C D , M N ∥ C D ⇒ P Q ∥ M N . Vậy tứ giác MNPQ là hình thang.
Ta có P Q = A B = 8 $ , M N = 1 2 A B = 4, M Q = N P = 1 2 S A = 3 . Vậy MNPQ là hình thang cân.
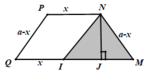
Gọi H là chân đường cao hạ từ đỉnh M của hình thang MNPQ. Khi đó ta có
H Q = 1 4 P Q = 2 ⇒ M H = M Q 2 − H Q 2 = 5
Vậy diện tích của thiết diện cần tìm là S = ( M N + P Q ) M H 2 = 6 5 .
