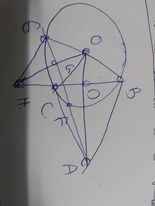
Cho đường tròn (O) bán kính R = 2 cm. Điểm A nằm ngoài đường tròn. Từ A vẽ các tiếp tuyến AB,AC với đường tròn (B,C là các tiếp điểm). AO cắt BC tại D. ( VẼ HÌNH HỘ MÌNH ) a) Cmr 4 điểm A,B,O,C cùng thuộc 1 đường tròn và OA là trung trực của BC (Ý 1 CM THEO 2 TAM GIÁC NỘI TIẾP, KHI CM NÊU RÕ NHỮNG DỮ KIỆN ĐỀ BÀI CHO) b) Vẽ đk BE của đường tròn (O), AE cắt đt (O) tại điểm thứ hai F. Gọi G là trung điểm của EF. Đt OG cắt đt BC tại H. Tính tích OA.OD và cm OA.OD=OG.OH c) CM EH là tiếp tuyến của đt (O)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Bổ sung đề; OA cắt BC tại D
a: Ta có: ΔOBA vuông tại B
=>B nằm trên đường tròn đường kính OA(1)
Ta có: ΔOCA vuông tại C
=>C nằm trên đường tròn đường kính OA(2)
Từ (1) và (2) suy ra B,C,O,A cùng thuộc đường tròn đường kính OA
Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(3)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(4)
Từ (3) và (4) suy ra OA là đường trung trực của BC
b: OA là đường trung trực của BC
Do đó: OA\(\perp\)BC tại D và D là trung điểm của BC
Xét ΔOBA vuông tại B có BD là đường cao
nên \(OD\cdot OA=OB^2=R^2\)
Ta có: ΔOEF cân tại O
mà OG là đường trung tuyến
nên OG\(\perp\)EF tại G
Xét ΔOGA vuông tại G và ΔODH vuông tại D có
góc GOA chung
Do đó: ΔOGA đồng dạng với ΔODH
=>\(\dfrac{OG}{OD}=\dfrac{OA}{OH}\)
=>\(OG\cdot OH=OA\cdot OD\)
c: Ta có: \(OG\cdot OH=OA\cdot OD\)
\(OA\cdot OD=R^2\)
Do đó: \(OG\cdot OH=R^2=OE^2\)
=>\(\dfrac{OG}{OE}=\dfrac{OE}{OH}\)
Xét ΔOGE và ΔOEH có
\(\dfrac{OG}{OE}=\dfrac{OE}{OH}\)
\(\widehat{GOE}\) chung
Do đó: ΔOGE đồng dạng với ΔOEH
=>\(\widehat{OGE}=\widehat{OEH}\)
=>\(\widehat{OEH}=90^0\)
=>HE là tiếp tuyến của (O)

a: góc KOA+góc BOA=90 độ
góc KAO+góc COA=90 độ
mà góc BOA=góc COA
nên góc KOA=góc KAO
=>ΔKAO cân tại K
b: Xét ΔOBA vuông tại B có sin BAO=OB/OA=1/2
nên góc BAO=30 độ
=>góc BOA=60 độ
Xét ΔOBI có OB=OI và góc BOI=60 độ
nên ΔOBI đều
=>OI=OB=1/2OA=R
=>I là trung điểm của OA
ΔKAO cân tại K
mà KI là trung tuyến
nên KI vuông góc với OI
=>KI là tiếp tuyến của (O)

a: Xét tứ giácc ABOC có
góc OBA+góc OCA=180 độ
nen ABOC là tứ giác nội tiếp
b: Xét ΔCAO vuông tại C và ΔCDE vuông tại C có
góc CAO=góc CDE
Do đó: ΔCAO đồng dạng vơi ΔCDE
=>CA/CD=CO/CE
=>CA/CO=CD/CE
Xét ΔCAD và ΔCOE có
CA/CO=CD/CE
góc ACD=góc OCE
Do đo: ΔCAD đồng dạng với ΔCOE


câu c thì cơ bản là tui chứng minh hai tam giác bằng nhau (c-c-c), xong rồi tui suy ra hai góc bằng nhau

a: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
=>ΔABC cân tại A
mà OB=OC
nên OA là trung trực của BC
b: ΔOEF cân tại O
mà OG là trung tuyến
nên OG vuông góc với EF
Xét ΔAGO vuông tại G và ΔHDO vuông tại D có
góc AOG chung
Do đó: ΔAGO đồng dạng với ΔHDO
c: ΔAGO đồng dạng vơi ΔHDO
=>OA/OH=OG/OD
=>OA*OD=OH*OG
=>OH*OG=OE^2
=>ΔHEO vuông tại E
=>HE là tiếp tuyên của (O)