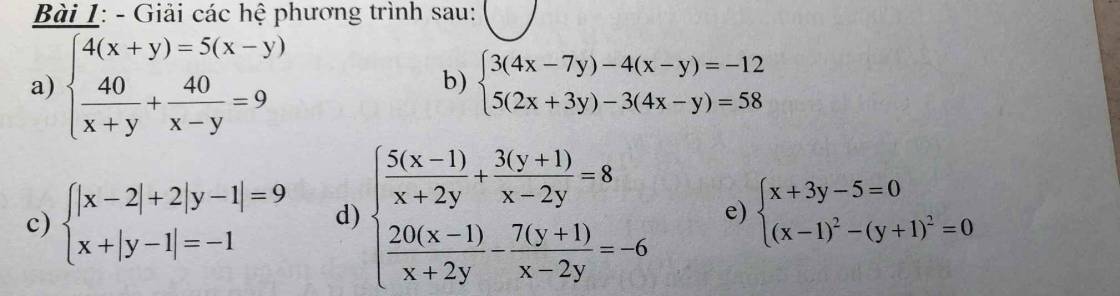cíu zứi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
cíu zứi
CT
11 tháng 2 2022
\(\dfrac{8\times3\times4}{16\times3}\)
\(=\dfrac{8\times3\times2\times2}{8\times2\times3}\)
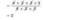
b) \(\dfrac{30\times25\times7\times8}{75\times8\times12\times14}\)
9 tháng 2 2022
a: 3/5=9/15
7/3=35/15
b: 9/10=36/40
5/4=50/40
c: 2/7=8/28
5/4=35/28
d: 8/9=16/18
11/6=33/18
e: 6/5=48/40
13/8=65/40
g: 4/5=8/10
3/2=15/10
h: 5/12=10/24
7/8=21/24
i: 11/4=33/12
13/6=26/12
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
8 tháng 2 2022
Bài 2:
\(a,\dfrac{2\times6\times13}{5\times13\times6}=\dfrac{2}{5}\\ b,\dfrac{8\times11\times13}{11\times13\times16}=\dfrac{8}{16}=\dfrac{8}{8\times2}=\dfrac{1}{2}\\ c,\dfrac{5\times18\times12}{15\times24\times16}=\dfrac{5\times3\times3\times6\times3\times4}{3\times5\times4\times6\times4\times4}=\dfrac{3\times3}{4\times4}=\dfrac{9}{16}\\ d,\dfrac{15\times8\times4}{32\times3\times5}=\dfrac{5\times3\times8\times4}{4\times8\times3\times5}=\dfrac{1}{1}=1\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
8 tháng 2 2022
Bài 1:
\(a,\dfrac{8}{12}=\dfrac{8:4}{12:4}=\dfrac{2}{3}\\ \dfrac{20}{48}=\dfrac{20:4}{48:4}=\dfrac{5}{12}\\ \dfrac{74}{100}=\dfrac{74:2}{100:2}=\dfrac{37}{50}\\ \dfrac{18}{21}=\dfrac{18:3}{21:3}=\dfrac{6}{7}\\ \dfrac{40}{54}=\dfrac{40:2}{54:2}=\dfrac{20}{27}\\ \dfrac{30}{45}=\dfrac{30:15}{45:3}=\dfrac{2}{3}\\ b,\dfrac{18}{24}=\dfrac{18:6}{24:6}=\dfrac{3}{4}\\ \dfrac{49}{28}=\dfrac{49:7}{28:7}=\dfrac{7}{4}\\ \dfrac{15}{35}=\dfrac{15:5}{35:5}=\dfrac{3}{7}\\ \dfrac{28}{40}=\dfrac{28:4}{40:4}=\dfrac{7}{10}\\ \dfrac{36}{27}=\dfrac{36:9}{27:9}=\dfrac{4}{3}\\ \dfrac{56}{49}=\dfrac{56:7}{49:7}=\dfrac{8}{7}\)
\(c,\dfrac{85}{51}=\dfrac{85:17}{51:17}=\dfrac{5}{3}\\ \dfrac{1515}{2323}=\dfrac{1515:101}{2323:101}=\dfrac{15}{23}\\ \dfrac{39}{26}=\dfrac{39:13}{26:13}=\dfrac{3}{2}\\ \dfrac{323232}{515151}=\dfrac{323232:10101}{515151:10101}=\dfrac{32}{51}\)
HM
2
4 tháng 1
có 2xy +x +y = 7
(2xy + x)+y = 7
x. (2+y)+1.(2+y)=9
(2+y) . (x+1) = 9
Mà x;y E Z =>2+y ; x+1 E Z
=>2+y ; x+1 E ư (9)={1 ; -1 ; 3 ; -3 ; 9 ; -9}
BGT
| x+1 | 1 | -1 | 3 | -3 | 1 | -1 | 9 | -9 | 3 | -3 |
| x | 0 | -2 | 2 | -4 | 0 | -2 | 8 | -10 | 2 | -4 |
| 2+y | 3 | -3 | 1 | -1 | 9 | -9 | 1 | -1 | 9 | -9 |
| y | 1 | -5 | -1 | -3 | 7 | -11 | -1 | -3 | 7 | -11 |
vậy (x;y)=(0;1) ; (-2;-5) ; (2;-1) ; (-4;-3) ; (0;7) ; (-2;-11) ; (8;-1) ; (-10;-3) ; (2;7) ; (-4;-11)
mik là ng trả lời đầu tiên nên cũng ko chắc lắm nhé bn :>>
4 tháng 1
2xy + x + y = 7
x(2y + 1) + y = 7
2.[x(2y +1) + y ] = 2.7
2x(2y + 1) + 2y = 14
2x(2y+1) + 2y + 1 = 14 +1
2x(2y+1) + (2y +1) = 15
(2y+1).(2x+1) = 15
Vì x, y thuộc Z nên 2x+1 và 2y+1 là ước của 15
*(mình làm đến đây bạn tự kẻ bảng nhé)
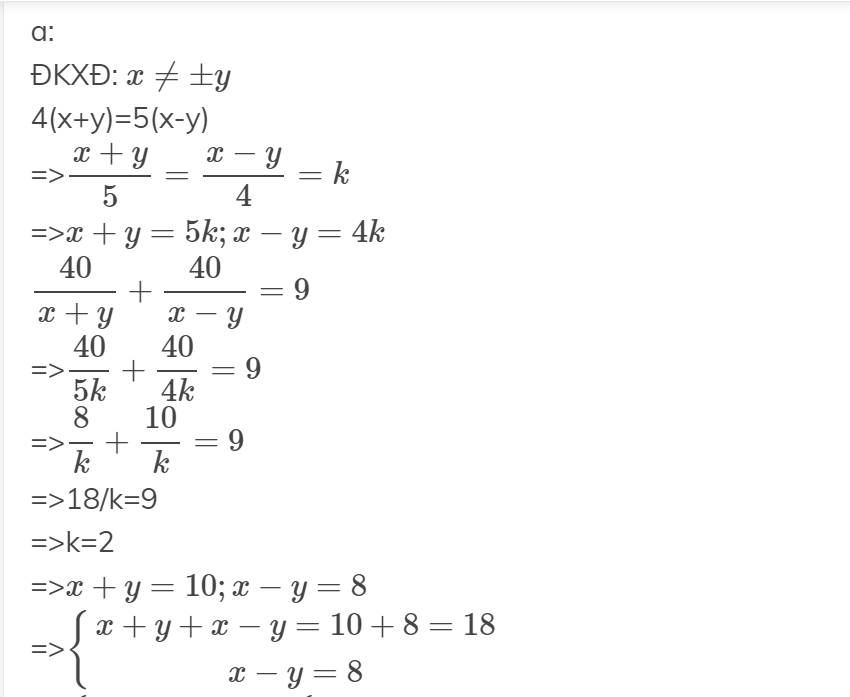
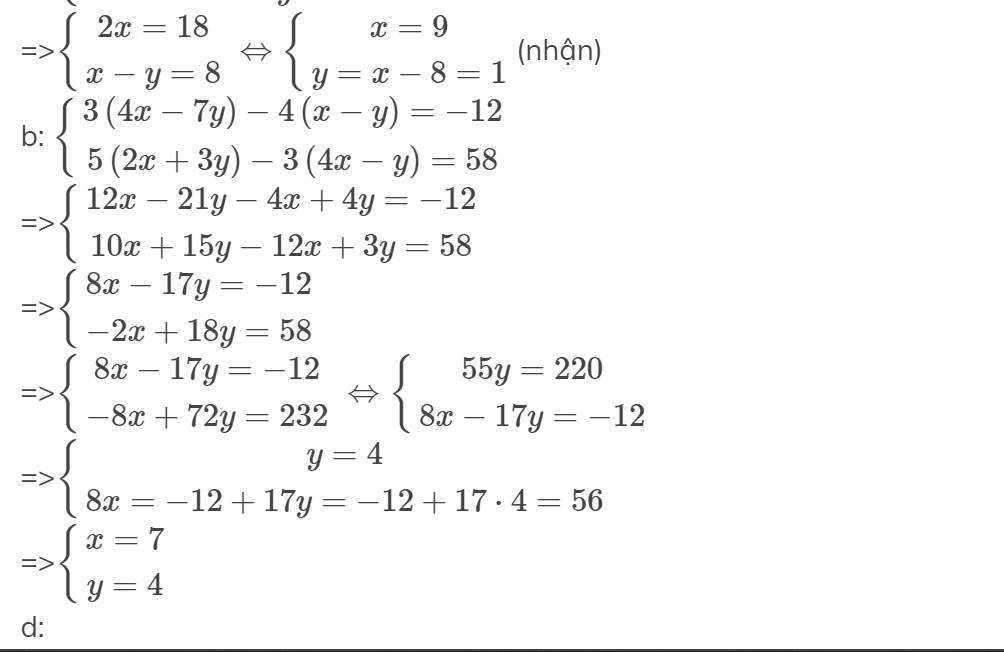
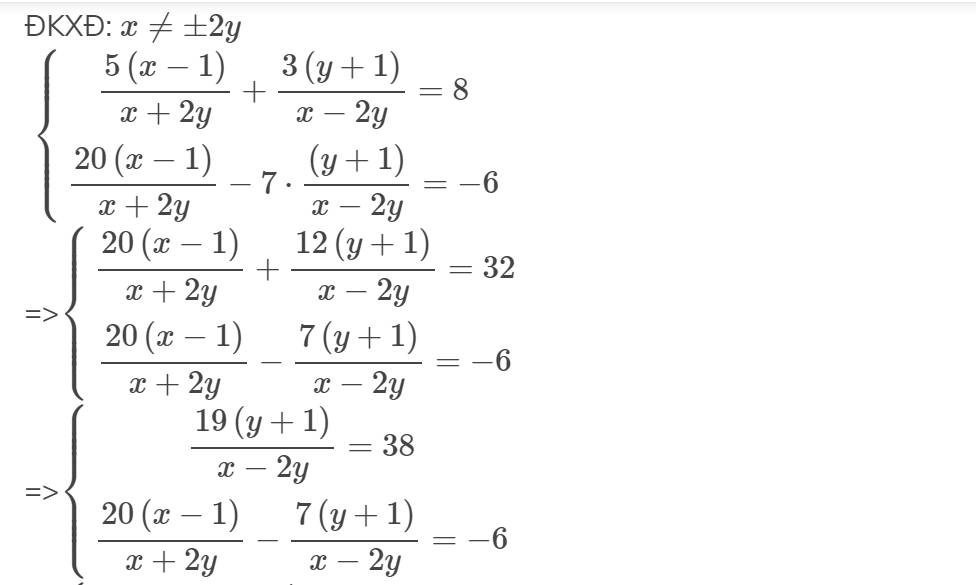
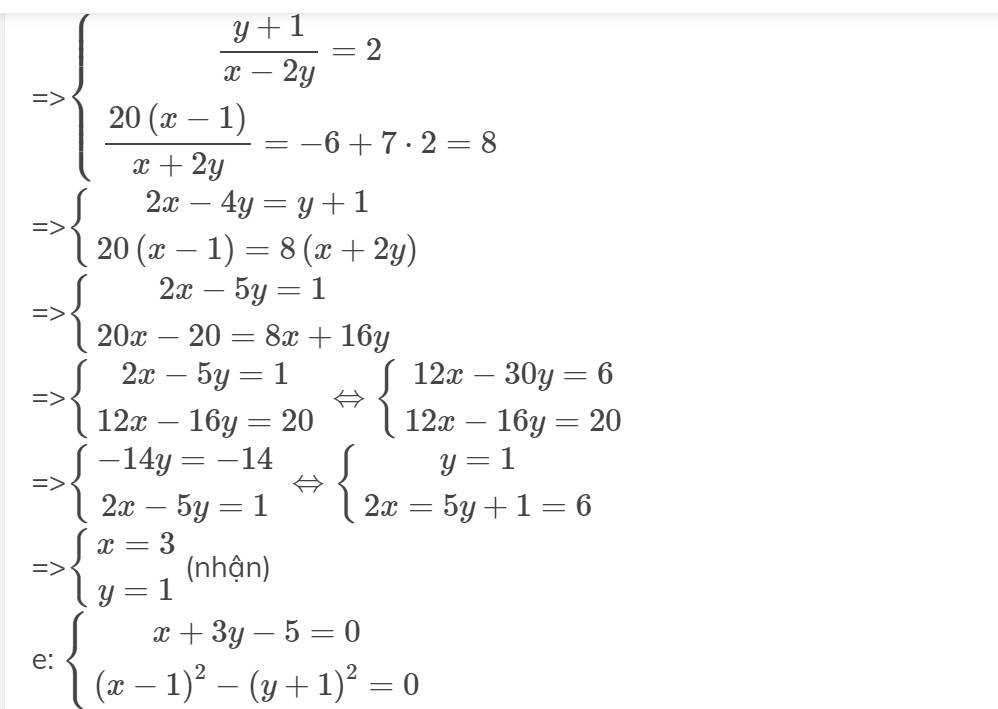
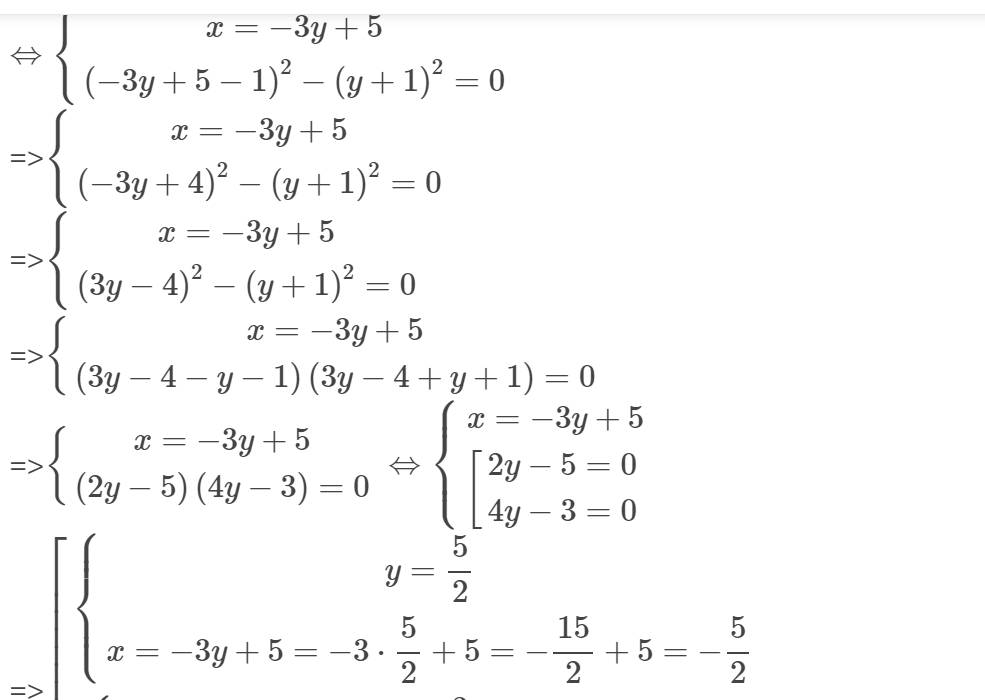
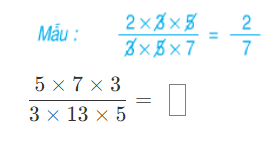
a:
ĐKXĐ: \(x\ne\pm y\)
4(x+y)=5(x-y)
=>\(\dfrac{x+y}{5}=\dfrac{x-y}{4}=k\)
=>\(x+y=5k;x-y=4k\)
\(\dfrac{40}{x+y}+\dfrac{40}{x-y}=9\)
=>\(\dfrac{40}{5k}+\dfrac{40}{4k}=9\)
=>\(\dfrac{8}{k}+\dfrac{10}{k}=9\)
=>18/k=9
=>k=2
=>\(x+y=10;x-y=8\)
=>\(\left\{{}\begin{matrix}x+y+x-y=10+8=18\\x-y=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=18\\x-y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=9\\y=x-8=1\end{matrix}\right.\)(nhận)
b: \(\left\{{}\begin{matrix}3\left(4x-7y\right)-4\left(x-y\right)=-12\\5\left(2x+3y\right)-3\left(4x-y\right)=58\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12x-21y-4x+4y=-12\\10x+15y-12x+3y=58\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x-17y=-12\\-2x+18y=58\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x-17y=-12\\-8x+72y=232\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}55y=220\\8x-17y=-12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=4\\8x=-12+17y=-12+17\cdot4=56\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=7\\y=4\end{matrix}\right.\)
d:
ĐKXĐ: \(x\ne\pm2y\)
\(\left\{{}\begin{matrix}\dfrac{5\left(x-1\right)}{x+2y}+\dfrac{3\left(y+1\right)}{x-2y}=8\\\dfrac{20\left(x-1\right)}{x+2y}-7\cdot\dfrac{\left(y+1\right)}{x-2y}=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{20\left(x-1\right)}{x+2y}+\dfrac{12\left(y+1\right)}{x-2y}=32\\\dfrac{20\left(x-1\right)}{x+2y}-\dfrac{7\left(y+1\right)}{x-2y}=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{19\left(y+1\right)}{x-2y}=38\\\dfrac{20\left(x-1\right)}{x+2y}-\dfrac{7\left(y+1\right)}{x-2y}=-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{y+1}{x-2y}=2\\\dfrac{20\left(x-1\right)}{x+2y}=-6+7\cdot2=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-4y=y+1\\20\left(x-1\right)=8\left(x+2y\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-5y=1\\20x-20=8x+16y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-5y=1\\12x-16y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}12x-30y=6\\12x-16y=20\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-14y=-14\\2x-5y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\2x=5y+1=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)(nhận)
e: \(\left\{{}\begin{matrix}x+3y-5=0\\\left(x-1\right)^2-\left(y+1\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-3y+5\\\left(-3y+5-1\right)^2-\left(y+1\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3y+5\\\left(-3y+4\right)^2-\left(y+1\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3y+5\\\left(3y-4\right)^2-\left(y+1\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3y+5\\\left(3y-4-y-1\right)\left(3y-4+y+1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3y+5\\\left(2y-5\right)\left(4y-3\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3y+5\\\left[{}\begin{matrix}2y-5=0\\4y-3=0\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}y=\dfrac{5}{2}\\x=-3y+5=-3\cdot\dfrac{5}{2}+5=-\dfrac{15}{2}+5=-\dfrac{5}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}y=\dfrac{3}{4}\\x=-3y+5=-3\cdot\dfrac{3}{4}+5=-\dfrac{9}{4}+5=\dfrac{11}{4}\end{matrix}\right.\end{matrix}\right.\)
c: TH1: x>=2
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}x-2+2\left|y-1\right|=9\\x+\left|y-1\right|=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+2\left|y-1\right|=11\\x+\left|y-1\right|=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left|y-1\right|=12\\x+\left|y-1\right|=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1-12=-13\left(loại\right)\\\left|y-1\right|=12\end{matrix}\right.\)
=>Loại
TH2: x<2
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}-x+2+2\left|y-1\right|=9\\x+\left|y-1\right|=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-x+2\left|y-1\right|=7\\x+\left|y-1\right|=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3\left|y-1\right|=6\\x+\left|y-1\right|=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left|y-1\right|=2\\x=-1-2=-3\left(nhận\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3\\\left[{}\begin{matrix}y-1=2\\y-1=-2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\\left[{}\begin{matrix}y=3\\y=-1\end{matrix}\right.\end{matrix}\right.\)