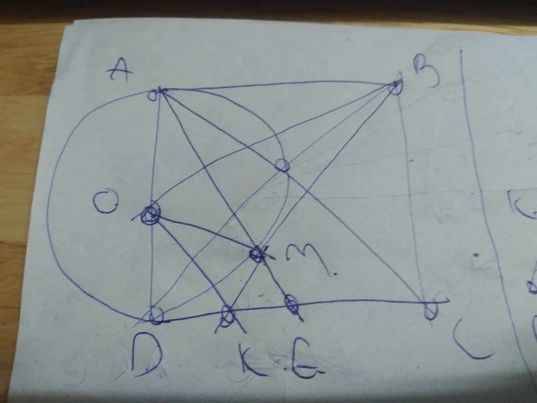
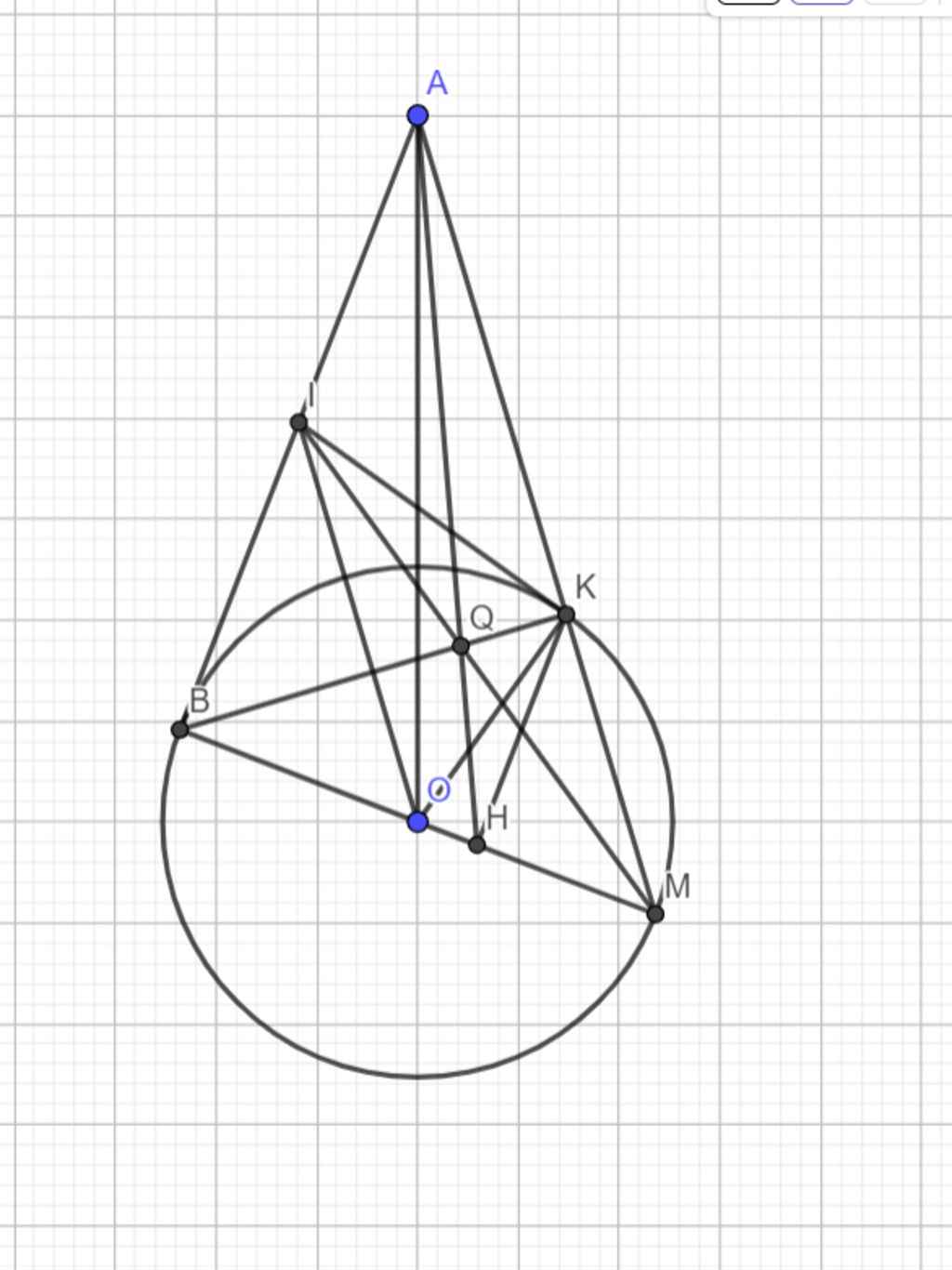
Cho hình vuông ABCD có độ dài cạnh bằng 4cm. Vẽ đường tròn tâm O đường kính AD, kẻ BM là tiếp tuyến của đường tròn O ( M là tiếp điểm, M khác A), BM cắt CD tại K a) Cm 4 điểm A,B,M,O cùng thuộc 1 đg tròn ( cm: 2 tam nội tiếp) b) Chứng minh OB vuông góc OK và BM.MK= AB^2/4 c) Đường thẳng AM cắt CD tại E. Cm K là trung điểm của ED và tính chu vi tứ giác ABKD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
AD là đường kính
AB\(\perp\)AD tại A
Do đó: AB là tiếp tuyến của (O)
Xét tứ giác AOMB có \(\widehat{OAB}+\widehat{OMB}=90^0+90^0=180^0\)
nên AOMB là tứ giác nội tiếp
=>A,O,M,B cùng thuộc một đường tròn
b: Xét (O) có
OD là bán kính
DK\(\perp\)DO tại D
Do đó: DK là tiếp tuyến của (O)
Xét (O) có
BA,BM là các tiếp tuyến
Do đó: OB là phân giác của góc AOM
=>\(\widehat{AOM}=2\cdot\widehat{MOB}\)
Xét (O) có
KM,KD là các tiếp tuyến
Do đó: OK là phân giác của góc DOM
=>\(\widehat{DOM}=2\cdot\widehat{KOM}\)
Ta có: \(\widehat{MOA}+\widehat{MOD}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{KOM}+\widehat{BOM}\right)=180^0\)
=>\(2\cdot\widehat{KOB}=180^0\)
=>\(\widehat{KOB}=90^0\)
=>OK\(\perp\)OB
Xét (O) có
BA,BM là các tiếp tuyến
Do đó: BA=BM
Xét (O) có
KD,KM là các tiếp tuyến
Do đó: KD=KM
Xét ΔOBK vuông tại O có OM là đường cao
nên \(BM\cdot MK=OM^2\)
=>\(BM\cdot MK=\left(\dfrac{1}{2}AD\right)^2=\dfrac{1}{4}AD^2=\dfrac{1}{4}AB^2\)
c: Ta có: BA=BM
=>B nằm trên đường trung trực của AM(1)
Ta có: OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra BO là đường trung trực của AM
=>BO\(\perp\)AM
mà BO\(\perp\)OK
nên AM//OK
Xét ΔDEA có
O là trung điểm của AD
OK//AE
Do đó: K là trung điểm của DE

Ta có: ΔBAO vuông tại A
=>ΔBAO nội tiếp đường tròn đường kính BO
=>A nằm trên đường tròn đường kính BO(1)
Ta có: ΔBMO vuông tại M
=>ΔBMO nội tiếp đường tròn đường kính BO
=>M nằm trên đường tròn đường kính BO(2)
Từ (1),(2) suy ra A,B,M,O cùng thuộc đường tròn đường kính BO

a) Ta có \(I\) là trung điểm \(AB,O\) là trung điểm \(BM\)
\(\rightarrow IO\) là đường trung bình \(\Delta ABM\rightarrow OI\text{/ / }AM\rightarrow OI\text{/ / }KM\)
Vì \(BM\) là đường kính của \(O\)\(\rightarrow BK\text{⊥}KM\rightarrow OI\text{⊥}BK\)
\(\rightarrow B,K\) đối xứng qua \(OI\)
\(\rightarrow\widehat{IKO=\widehat{IBO}=90^o}\)
\(\rightarrow IK\) là tiếp tuyền của \(O\)
Biết mỗi làm câu A

a) Vì AB là đường kính \(\Rightarrow\angle AMB=90\Rightarrow\angle ACD=\angle AMD=90\)
\(\Rightarrow ACMD\) nội tiếp
b) Ta có: \(\angle KCB+\angle KMB=90+90=180\Rightarrow KCBM\) nội tiếp
\(\Rightarrow\angle AKC=\angle MBA\)
Ta có: \(\angle NMK=\angle MBA=\angle AKC=\angle MKN\)
\(\Rightarrow\Delta NMK\) cân tại N
c) Vì B và E đối xứng với nhau qua C \(\Rightarrow\) CD là trung trực BE
\(\Rightarrow\angle DEC=\angle DBC=\angle AKC\Rightarrow AKDE\) nội tiếp

a: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét (O) có
ΔDMC nội tiếp
DC là đường kính
Do đó: ΔDMC vuông tại M
=>CM\(\perp\)MD tại M
=>CM\(\perp\)AD tại M
Xét tứ giác AMHC có \(\widehat{AMC}=\widehat{AHC}=90^0\)
nên AMHC là tứ giác nội tiếp
a: Xét (O) có
AD là đường kính
AB\(\perp\)AD tại A
Do đó: AB là tiếp tuyến của (O)
Xét tứ giác AOMB có \(\widehat{OAB}+\widehat{OMB}=90^0+90^0=180^0\)
nên AOMB là tứ giác nội tiếp
=>A,O,M,B cùng thuộc một đường tròn
b: Xét (O) có
OD là bán kính
DK\(\perp\)DO tại D
Do đó: DK là tiếp tuyến của (O)
Xét (O) có
BA,BM là các tiếp tuyến
Do đó: OB là phân giác của góc AOM
=>\(\widehat{AOM}=2\cdot\widehat{MOB}\)
Xét (O) có
KM,KD là các tiếp tuyến
Do đó: OK là phân giác của góc DOM
=>\(\widehat{DOM}=2\cdot\widehat{KOM}\)
Ta có: \(\widehat{MOA}+\widehat{MOD}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{KOM}+\widehat{BOM}\right)=180^0\)
=>\(2\cdot\widehat{KOB}=180^0\)
=>\(\widehat{KOB}=90^0\)
=>OK\(\perp\)OB
Xét (O) có
BA,BM là các tiếp tuyến
Do đó: BA=BM
Xét (O) có
KD,KM là các tiếp tuyến
Do đó: KD=KM
Xét ΔOBK vuông tại O có OM là đường cao
nên \(BM\cdot MK=OM^2\)
=>\(BM\cdot MK=\left(\dfrac{1}{2}AD\right)^2=\dfrac{1}{4}AD^2=\dfrac{1}{4}AB^2\)
c: Ta có: BA=BM
=>B nằm trên đường trung trực của AM(1)
Ta có: OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra BO là đường trung trực của AM
=>BO\(\perp\)AM
mà BO\(\perp\)OK
nên AM//OK
Xét ΔDEA có
O là trung điểm của AD
OK//AE
Do đó: K là trung điểm của DE
Vẽ hình hộ mình nhé bạn