giúp em 7 bài này với ạ:(
sáng mai phải nộp bài rồi ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HK
3
31 tháng 10 2021
Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi
29 tháng 8 2021
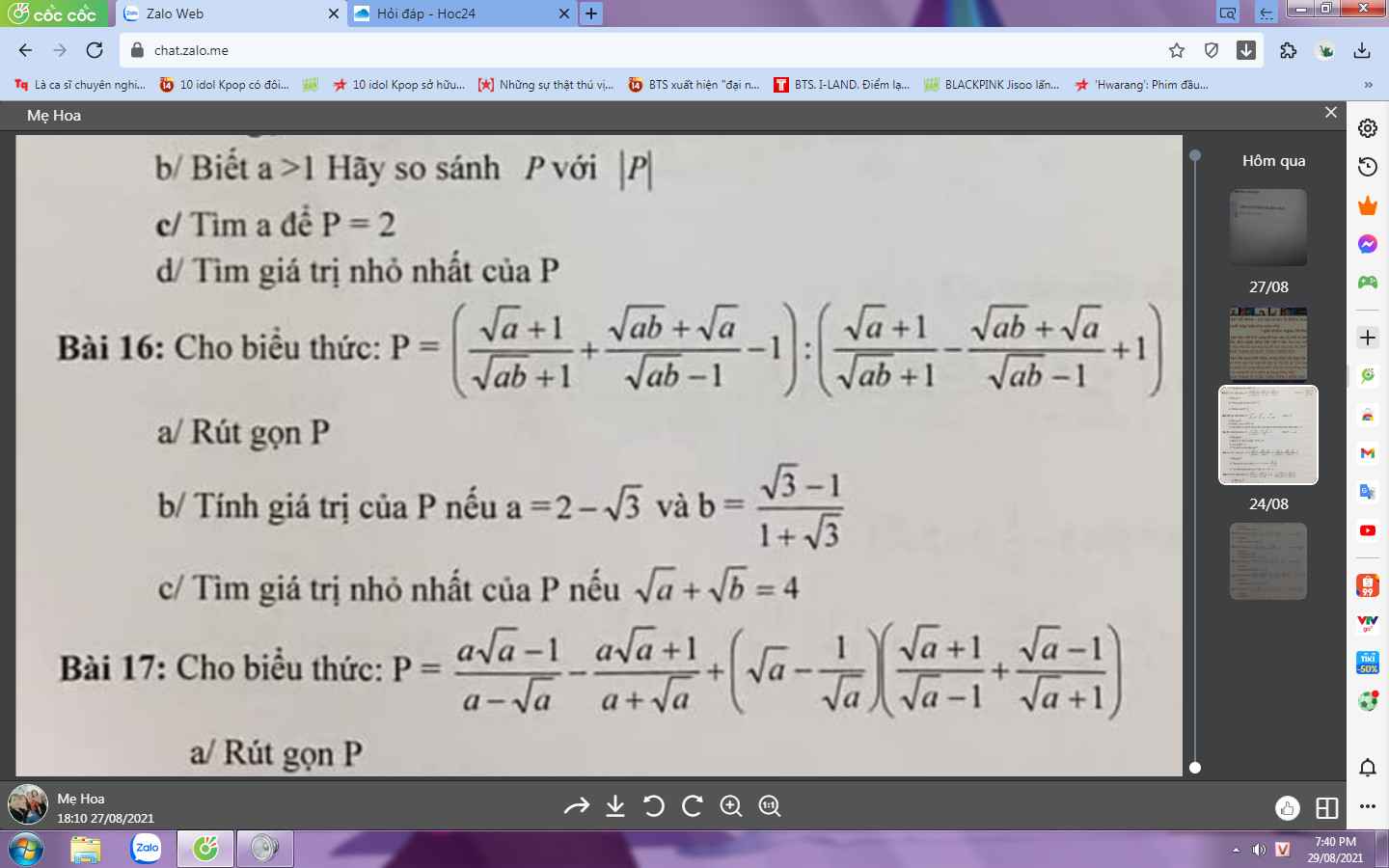
Bài 16:
a: Ta có: \(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}+\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}-1\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}-\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}+1\right)\)
\(=\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1+ab+\sqrt{ab}+a\sqrt{b}+\sqrt{a}-ab+1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}:\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1-ab-\sqrt{ab}-a\sqrt{b}-\sqrt{a}+ab-1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}\)
\(=\dfrac{2a\sqrt{b}+2\sqrt{ab}}{-2\sqrt{a}-2}\)
\(=\dfrac{2\sqrt{ab}\left(\sqrt{a}+1\right)}{-2\left(\sqrt{a}+1\right)}\)
\(=-\sqrt{ab}\)
9 tháng 11 2023
Gọi tia đối của tia AB là AE
=>AD là phân giác của \(\widehat{EAC}\)
Xét ΔABC có \(\widehat{EAC}\) là góc ngoài tại đỉnh A
nên \(\widehat{EAC}=\widehat{ABC}+\widehat{ACB}=80^0\)
AD là phân giác của góc EAC
=>\(\widehat{EAD}=\widehat{CAD}=\dfrac{\widehat{EAC}}{2}=\dfrac{80^0}{2}=40^0\)
\(\widehat{DAC}=\widehat{ACB}\left(=40^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
Mọi người giúp em câu này gấp với ạ, sáng mai em phải trả bài rồi. Em cảm ơn mọi người rất nhiều!
TK
1
19 tháng 9 2018
=> 1 - 3 . X=x - 7 hoặc 1 - 3 . X =-(x-7)
*1 - 3x =x - 7 *1 - 3x = -(x - 7 )
8 =x + 3x 1 - 3x = -x + 7
8 =4x -3x+x =7-1
8 : 4 =x -2x =6
2 = x x = 6:(-2)
=>x = 2 x = -3
vậy x \(\in\){2; -3}
đúng + x =1
x =1 -đúng
x = thích
GC
4
MH
14 tháng 11 2021
\(A=\left(-1\right)+2-3+\left(-4\right)+5-6+\left(-7\right)+8-9\)
\(=2-1-3+5-4-6+8-7-9\)
\(=\left(2-1-3\right)+\left(5-4-6\right)+\left(8-7-9\right)\)
\(=\left(-2\right)+\left(-5\right)+\left(-8\right)\)
\(=-15\)
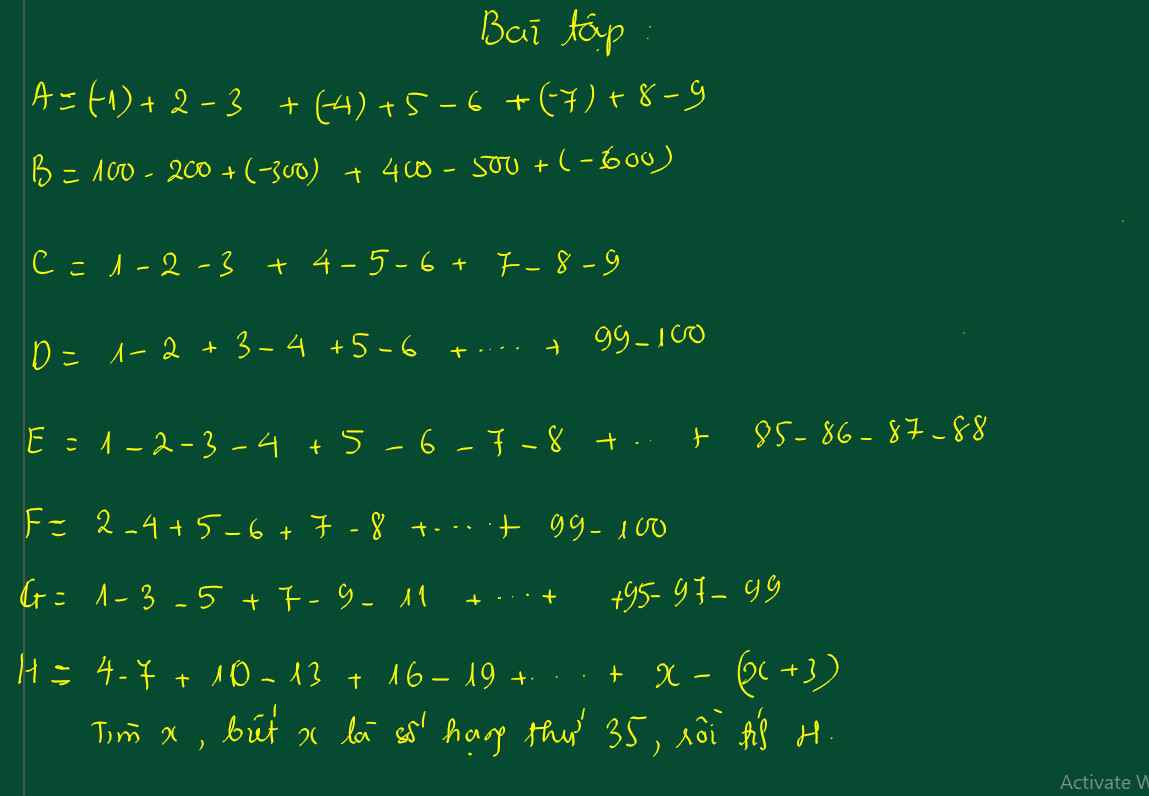
Bài 6:
Xét ΔOAC vuông tại A và ΔOBD vuông tại B có
OA=OB
\(\widehat{AOC}=\widehat{BOD}\)(hai góc đối đỉnh)
Do đó: ΔOAC=ΔOBD
=>OC=OD
Bài 7:
a: Ta có: \(\widehat{DAB}+\widehat{BAC}+\widehat{CAE}=180^0\)
=>\(\widehat{DAB}+\widehat{CAE}+90^0=180^0\)
=>\(\widehat{DAB}+\widehat{CAE}=90^0\)
mà \(\widehat{DAB}+\widehat{DBA}=90^0\)
nên \(\widehat{DBA}=\widehat{CAE}\)
Xét ΔABD vuông tại A và D và ΔCAE vuông tại E có
AB=AC
\(\widehat{DBA}=\widehat{EAC}\)
Do đó: ΔABD=ΔCAE
b: ta có: ΔABD=ΔCAE
=>DB=AE và AD=CE
DB+CE=DA+AE=DE