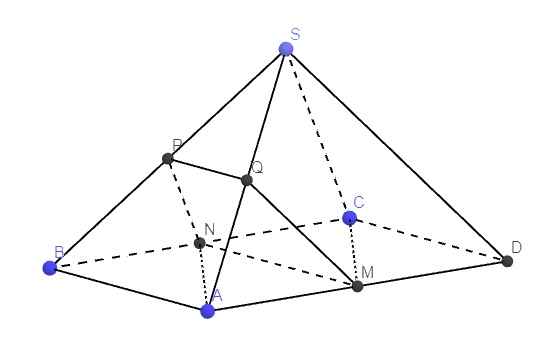
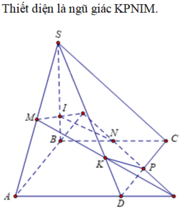
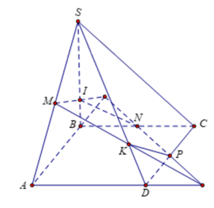
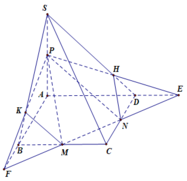
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của SA, BC, CD. Gọi giao điểm của SB và (MNP) là I. Tính tỉ số IS/IB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

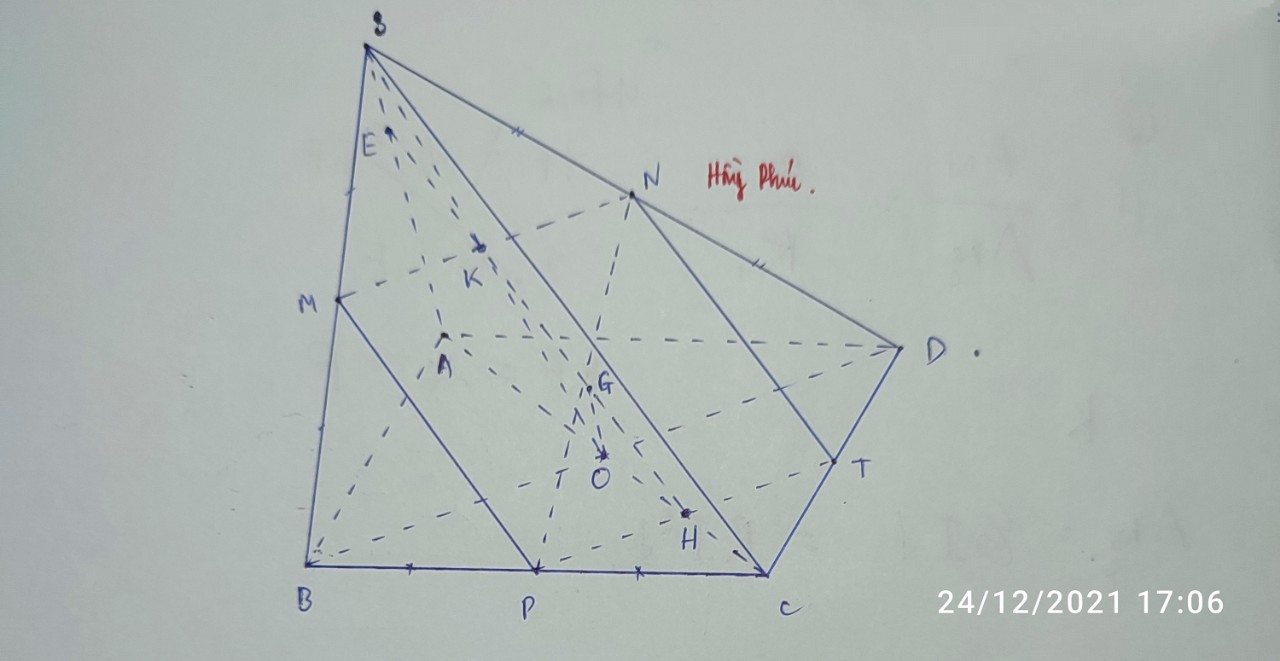
1: Gọi giao điểm của AC và BD là O trong mp(ABCD)
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên (SAC) giao (SBD)=SO
Xét ΔSDC có
P,N lần lượt là trung điểm của DS,DC
=>PN là đường trung bình của ΔSDC
=>PN//SC
PN//SC
SC\(\subset\)(SBC)
PN không nằm trong mp(SBC)
Do đó: PN//(SBC)

a. Do M, N là trung điểm AD, BC \(\Rightarrow MN||AB||CD\)
Gọi Q là trung điểm SA
\(\Rightarrow PQ\) là đường trung bình tam giác SAB
\(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow Q\in\left(MNP\right)\)
\(\Rightarrow Q=SA\cap\left(MNP\right)\)
b. Do Q là trung điểm SA, M là trung điểm AD
\(\Rightarrow MQ\) là đường trung bình tam giác SAD \(\Rightarrow MQ||SD\)
Mà \(MQ\in\left(MNP\right)\Rightarrow SD||\left(MNP\right)\)
Tương tự ta có \(NP||SC\) (đường trung bình) (1)
\(\left\{{}\begin{matrix}AM=NC=\dfrac{1}{2}AD\\AM||NC\end{matrix}\right.\) \(\Rightarrow AN||CM\) (2)
(1);(2) \(\Rightarrow\left(SMC\right)||\left(ANP\right)\)
c. Đề bài không tồn tại điểm L