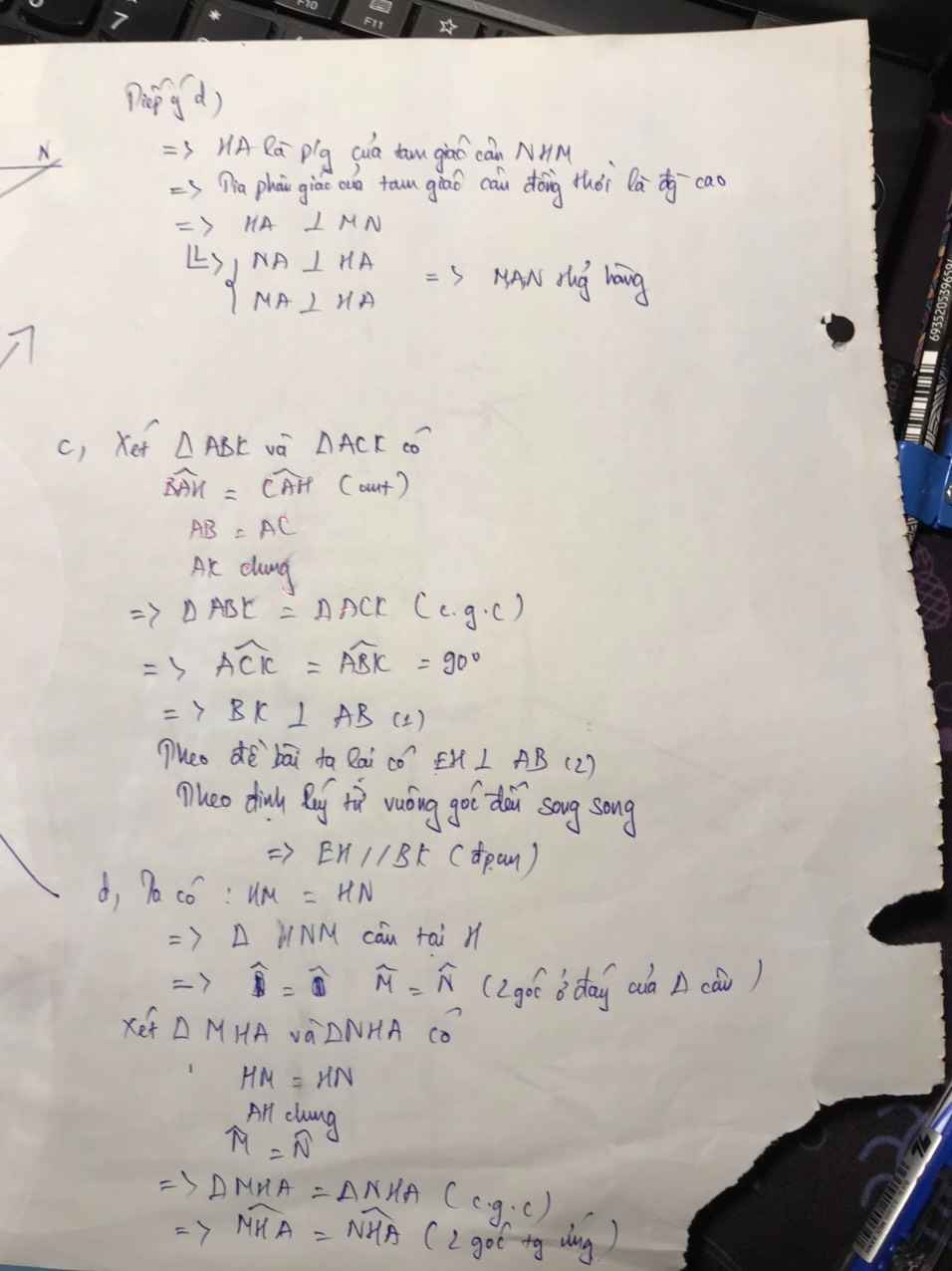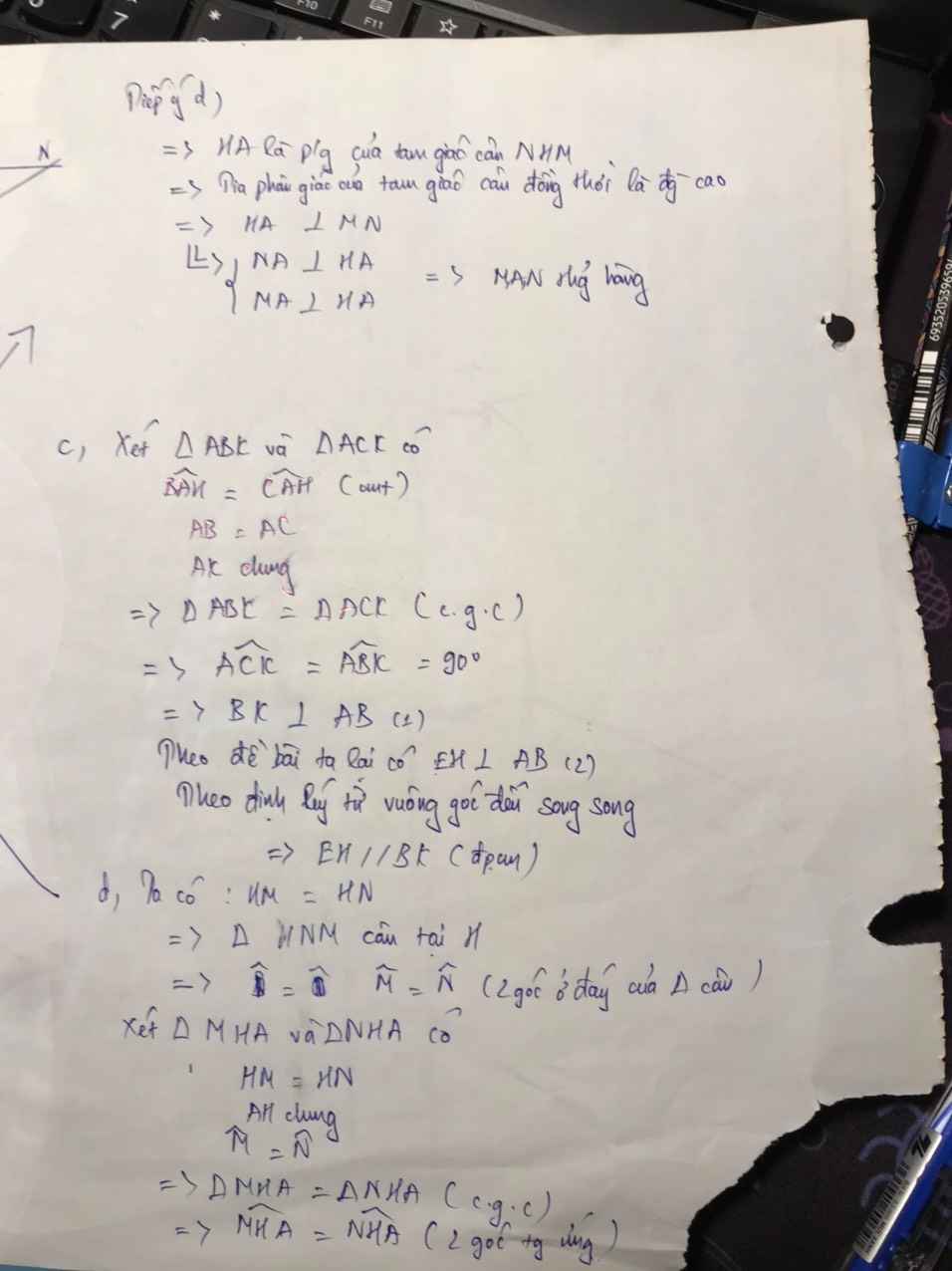Cho tam giác ABC vuông cân tại A. Lấy M bất kỳ trên AB, từ A vẽ đường thẳng vuông góc với CM cắt BC tại E. Gọi F là điểm đối xứng của B qua E. Từ F vẽ đường thẳng vuông góc với CM cắt AC tại K. Chứng minh tứ giác MKCB là hình thang cân.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

27 tháng 1 2023
a: Sửa đề: Cm góc BMK=góc CMD
góc BMK=90 độ-góc KBM
góc CMD=90 độ-góc MCD
mà góc KBM=góc MCD
nên góc BMK=góc CMD
=>góc BME=góc CMD
=>góc BME+góc BMD=180 độ
=>E,M,D thẳng hàng
b: K đối xứng E qua M
=>BK=BE; MK=ME
Xét ΔBKM và ΔBEM có
BK=BE
MK=ME
BM chung
=>ΔBKM=ΔBEM
=>góc BEM=góc BKM=90 độ
=>BE vuông góc ED
mà ED vuông góc DC
nên BE//DC
=>BE//HD
Xét tứ giác BEDH có
BE//HD
BH//DE
góc BHD=90 độ
=>BEDH là hình chữ nhật
c: MK=ME
=>MK+MD=ME+MD
=>MK+MD=ED=BH