Cho nửa đường tròn tâm O, đkinh AB. Vẽ các tiếp tuyến Ax, By của nửa đtron. Kẻ tiếp tuyến tại M là 1 điểm bất kì thuộc nửa đtron. Tiếp tuyến này cắt Ax, By tại C,D. CMR đtron đkinh CD tiếp xúc với AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


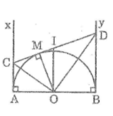
Theo tính chất tiếp tuyến, ta có:
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Suy ra tứ giác ABDC là hình thang
Gọi I là trung điểm của CD
Khi đó OI là đường trung bình của hình thang ABDC
Suy ra: OI // AC ⇒ OI ⊥ AB
Suy ra: IC = ID = IO = (1/2).CD (tính chất tam giác vuông)
Suy ra I là tâm đường tròn đường kính CD. Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.

Kẻ OI AB ( I CD) ta suy ra OI là đường trung bình của hình thang ABCD và CI = ID.
Khi đó I là tâm đường tròn đường kính CD và IO là khoảng cách d từ tâm I đến AB.
Ta có IO=CA+DB2 =MC+MD2 =DC2 là bán kính của đường tròn (I).
Do đó AB tiếp xúc với đường tròn đường kính CD.

c) BM cắt Ax tại E.BC cắt MH tại I
Vì AB là đường kính nên \(\angle AMB=90\)
Vì CM,CA là tiếp tuyến nên \(CM=CA\)
Ta có tam giác AME vuông tại M có \(CM=CA\Rightarrow C\) là trung điểm AE
Vì \(MH\parallel AE(\bot AB)\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{IH}{AC}=\dfrac{BI}{BC}\\\dfrac{IM}{CE}=\dfrac{BI}{BC}\end{matrix}\right.\Rightarrow\dfrac{IH}{AC}=\dfrac{IM}{CE}\)
mà \(AC=CE\Rightarrow IH=IM\) nên ta có đpcm
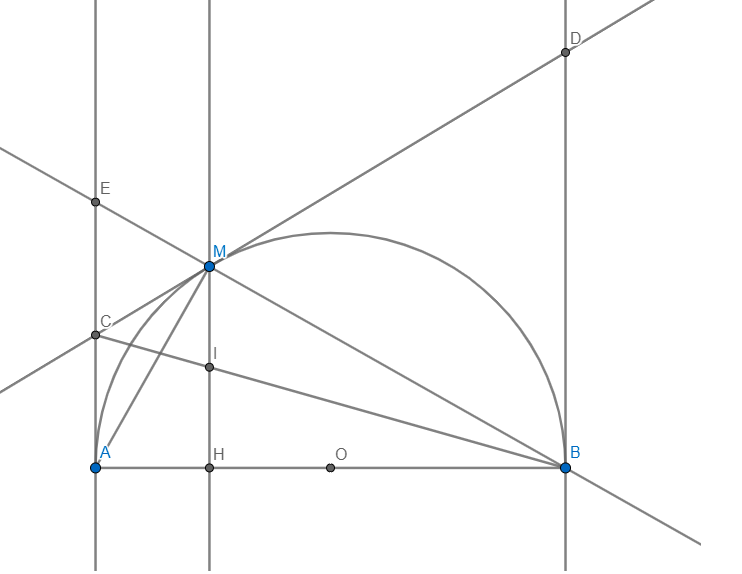

a: Xét (O) có
DM là tiếp tuyến
DA là tiếp tuyến
Do đó: OD là tia phân giác của góc MOA(1)
Xét (O) có
EM là tiếp tuyến
EB là tiếp tuyến
Do đó: OE là tia phân giác của góc MOB(2)
Từ (1) và (2) suy ra ΔDOE vuông tại O

a: Xét tứ giác ADMO có
góc DAO+góc DMO=180 độ
nên ADMO là tứ giác nội tiếp
b: Gọi N là trung điểm của CD
Xét hình thang ABCD ccó
O,N lần lượt là trung điểm của AB,CD
nên ON là đường trung bình
=>ON//AD//BC
=>ON vuông góc với AB
=>AB là tiếp tuyến của (N)
Xét (O) có
CA,CM là tiếp tuyến
Do đó: OC là phân giác của \(\widehat{MOA}\)
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
Xét (O) có
DM,DB là tiếp tuyến
Do đó: OD là phân giác của góc MOB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
\(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{MOD}+\widehat{MOC}\right)=180^0\)
=>\(2\cdot\widehat{DOC}=180^0\)
=>\(\widehat{DOC}=90^0\)
=>ΔDOC vuông tại O
Gọi N là trung điểm của CD
ΔOCD vuông tại O
=>ΔOCD nội tiếp đường tròn đường kính CD
mà N là trung điểm của CD
nên ΔOCD nội tiếp (N)
Xét hình thang ACDB có
O,N lần lượt là trung điểm của AB,CD
=>ON là đường trung bình của hình thang ACDB
=>ON//AC//BD
=>ON\(\perp\)AB tại O
Xét (N) có
NO là bán kính
AB\(\perp\)NO tại O
Do đó:AB là tiếp tuyến của (N)
=>Đường tròn đường kính CD tiếp xúc với AB