Hai xe chuyển động thẳng đều với vận tốc không đổi nếu đi ngược chiều thì sau 15 phút khoảng cách giữa hai xe là 25km. Nếu đi cùng chiều thì khoảng cách giữa hay xe là 5km. Tính vận tốc của mỗi xe
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 7 2017
Gọi v1; v2 lần lượt là vận tốc 2 xe.
s1; s2 lần lượt là quãng đường 2 xe đi được trong 2 trường hợp.
Theo bài ra ta có:
\(s_1=\left(v_1+v_2\right)t=25\Rightarrow v_1+v_2=\dfrac{25}{0,25}=100\left(\text{km/h}\right)\left(1\right)\)
Giả sử v1 > v2:
\(s_2=\left(v_1-v_2\right)t=5\Rightarrow v_1-v_2=\dfrac{5}{0,25}=20\left(\text{km/h}\right)\left(2\right)\)
Lấy (1)+(2); ta có: \(2v_1=120\Rightarrow v_1=60\left(\text{km/h}\right)\Rightarrow v_2=40\left(\text{km/h}\right)\)
Vậy......................
KH
1 tháng 7 2017
Hai xe chuyển động thẳng đều trên cùng một đường thẳng. Nếu đi ngược chiều thì sau 15 phút, khoảng cách giữa hai xe giảm 25km. Nếu đi cùng chiều thì sau 15 phút khỏng cách giữa hai xe chỉ giảm 5km. Tính vận tốc của mỗi xe.
Chọn chiều dương là chiều chuyển động của mỗi xe. Quãng đường mỗi xe đi được trong thời gian t: s1= v1.t ; s2 = v2.t
Khi đi ngược chiều, tổng quãng đường hai xe đi được chính là độ giảm khoảng cách:
s1 + s2 = (v1 + v2)t ⇒ \(\dfrac{v_1+v_2}{3}=25\) (1) Khi đi cùng chiều, hiệu quãng đường hai xe đi được chính là độ giảm về khoảng cách:
s2 − s1 = (v2 − v1)t ⇒ \(\dfrac{v_2-v_1}{3}=5\) (2) Từ (1) và (2) ta có hệ phương trình : \(\left\{{}\begin{matrix}v_1+v_2=25\\v_2-v_1=18\end{matrix}\right.\) Suy ra: v1 = 36 km/h ; v2 = 54 km/h. P/s: về phần này t chưa nắm kĩ rõ cho lém nên hỏi vài người này đê. @Như Khương Nguyễn, @Kayoko,. . . .
s1 + s2 = (v1 + v2)t ⇒ \(\dfrac{v_1+v_2}{3}=25\) (1) Khi đi cùng chiều, hiệu quãng đường hai xe đi được chính là độ giảm về khoảng cách:
s2 − s1 = (v2 − v1)t ⇒ \(\dfrac{v_2-v_1}{3}=5\) (2) Từ (1) và (2) ta có hệ phương trình : \(\left\{{}\begin{matrix}v_1+v_2=25\\v_2-v_1=18\end{matrix}\right.\) Suy ra: v1 = 36 km/h ; v2 = 54 km/h. P/s: về phần này t chưa nắm kĩ rõ cho lém nên hỏi vài người này đê. @Như Khương Nguyễn, @Kayoko,. . . .
KA
4 tháng 9 2017
Đổi 15 phút=1/4 h
Khi đi ngược chiều trong 15 phút tổng quãng đường 2 xe đi được là:
S1=1/4.(v1+v2)=25
=>v1+v2=100(km) (1)
Khi đi cùng chiều trong 15 phút khi đó khoảng cách giữa hai xe giảm 5km nên ta có:
1/4.(v1-v2)=5
=>v1-v2=20(km) (2)
Từ (1) và (2) giải hệ phương trình được v1=60(km/h) v2=40(km/h)
VT
20 tháng 2 2019
Chọn đáp án C
Gọi vận tốc của hai xe lần lượt là v 1 , v 2
Khi hai xe chuyển động ngược chiều thì
Khi hai xe chuyển động cùng chiều thì
TN
23 tháng 10 2019
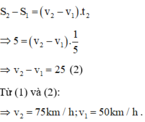
đổi 15p=1/4h
khi đi đc quãng đường trong vòng 15p thì lúc đó hai xe đi đc quãng đường là
s1=1/4.(v1+v2)=25(km)
=>v1+v2=100km (1)
khi đi ngược chiểu trong 15p thì khi đó quãng đường hai xe giảm 5km ta có
1/4.(v1-v2)=5(km)
=>v1-v2=20km (2)
từ (1) và (2) giải hệ phương trình ta đc v1=60km/h, v2=40km/h