Bài 4. (1 điểm) Cho hình chóp tứ giác đều $S.MNPQ$ như hình vẽ có chiều cao $15$ cm và thể tích là $1$ $280$ cm$^3$.
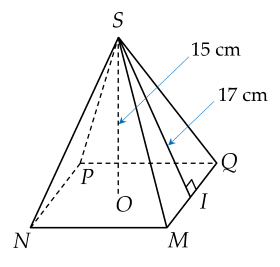
Tính độ dài cạnh đáy của hình chóp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 7 2023
a: Diện tích đáy là 1280:15=256/3(cm2)
Độ dài đáy là: \(\sqrt{\dfrac{256}{3}}=\dfrac{16}{\sqrt{3}}\left(cm\right)\)
b: \(Sxq=\dfrac{1}{2}\cdot17\cdot\dfrac{16}{\sqrt{3}}\cdot4\simeq78,52\left(cm^2\right)\)
H9
HT.Phong (9A5)
CTVHS
10 tháng 10 2023
Diện tích đáy của hình chóp tứ giá đều:
\(V=\dfrac{1}{3}Sh\Rightarrow S=\dfrac{3V}{h}=\dfrac{3\cdot13,5}{4,5}=9\left(cm^2\right)\)
Độ dài cạnh đáy là:
\(\sqrt{9}=3\left(cm\right)\)
21 tháng 10 2023
a: O ở đâu vậy bạn?
b: Diện tích đáy là \(6.5^2=42.25\left(cm^2\right)\)
Thể tích hình chóp là: \(V=\dfrac{1}{3}\cdot42.25\cdot12=169\left(cm^3\right)\)
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
a) Diện tích xung quanh của hình chóp tam giác đều là:
\(\frac{{99.40}}{2}.3 = 5940\) (\(c{m^2}\))
Diện tích đáy của hình chóp là:
\(\frac{{40.34,6}}{2} = 692\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là:
\(5940 + 692 = 6632\) (\(c{m^2}\))
Thể tích của hình chóp là:
\(\frac{1}{3}.692.98,3 \approx 22674,53\) (\(c{m^3}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là:
\(\frac{{91.120}}{2}.4 = 21840\) (\(c{m^2}\))
Diện tích đáy của hình chóp là:
\(120.120 = 14400\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là:
\(21840 + 14400 = 36240\) (\(c{m^2}\))
Thể tích của hình chóp là:
\(\frac{1}{3}.14400.68,4 = 328320\) (\(c{m^3}\))
\(V_{S.MNPQ}=\dfrac{1}{3}.S_{MNPQ}.SO\)
\(\Rightarrow S_{MNPQ}=\dfrac{3.V_{S.MNPQ}}{SO}=\dfrac{3.1280}{15}=256cm^2\)
Xét tg vuông SOI
\(OI=\sqrt{SI^2-SO^2}\) (Pitago)
\(\Rightarrow OI=\sqrt{17^2-15^2}=8cm\)
Ta có
\(OI=\dfrac{MN}{2}\Rightarrow MN=2.OI=2.8=16cm\)
Ta có:
\(V=\dfrac{1}{3}.S_{MNPQ}.15=1280\left(cm^3\right)\)
\(\Rightarrow S_{MNPQ}=\dfrac{1280.3}{15}=256\left(cm^2\right)\)
\(\Rightarrow MN=\sqrt{256}=16\left(cm\right)\)