Một con lắc lò xo treo thẳng đứng gồm lò xo có độ cứng k = 50N/m và vật có khối lượng m (g) dao động điều hòa theo phương thẳng đứng với li độ \(x=10\cos\left(5\pi t+\dfrac{\pi}{2}\right)\left(cm\right)\) biết g = 10 m/s2.
a) Tính khối lượng của vật và chu kỳ của con lắc
b) Tính thế năng, động năng và cơ năng của con lắc khi vật ở li độ x = 2 cm
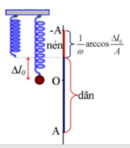
c) Tính lực đàn hội của lò xo khi vật nặng có \(v=\dfrac{1}{2}v_{max}\)


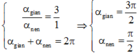
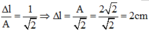
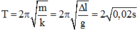
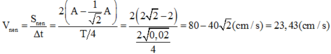
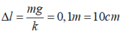

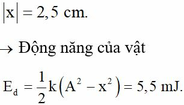

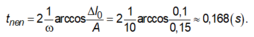
Giả sử: \(\pi^2\approx10\)
a) Khối lượng của vật: \(m=\dfrac{k}{\omega^2}=\dfrac{50}{\left(5\pi\right)^2}=0,2kg=200g\)
Chu kì của con lắc: \(T=\dfrac{2\pi}{\omega}=\dfrac{2}{5}\left(s\right)\)
b)Thế năng: \(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}\cdot50\cdot0,02^2=0,01J\)
Tại li độ \(x=2cm\) thì \(v=-\omega Asin\left(\pi t+\varphi\right)=-50\pi sin\left(5\pi t+\dfrac{\pi}{2}\right)\Rightarrow t\)
Động năng: \(W_đ=\dfrac{1}{2}mv^2\)
Cơ năng con lắc: \(W=W_đ+W_t=0,24J\)
a) \(k=m\omega^2=50\Rightarrow m=0,2\left(kg\right)\)
\(T=\dfrac{2\pi}{\omega}=0,4\left(s\right)\)
b) \(W_t=\dfrac{1}{2}kx^2=0,01\left(J\right)\)
\(W=\dfrac{1}{2}kA^2=0,25\left(J\right)\)
\(W_đ=W-W_t=0,24\left(J\right)\)
c) \(\Delta l=\dfrac{mg}{k}=0,04\left(m\right)\)
\(v=\dfrac{1}{2}v_{max}\Rightarrow x=\dfrac{A\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)=0,05\sqrt{3}\left(m\right)\)
\(F_{đh}=k\left(\Delta l+x\right)\approx6,33\left(N\right)\)