 chi tiết ko cần vẽ hình làm theo chương trinh mới ạ gấp lắm
chi tiết ko cần vẽ hình làm theo chương trinh mới ạ gấp lắm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40
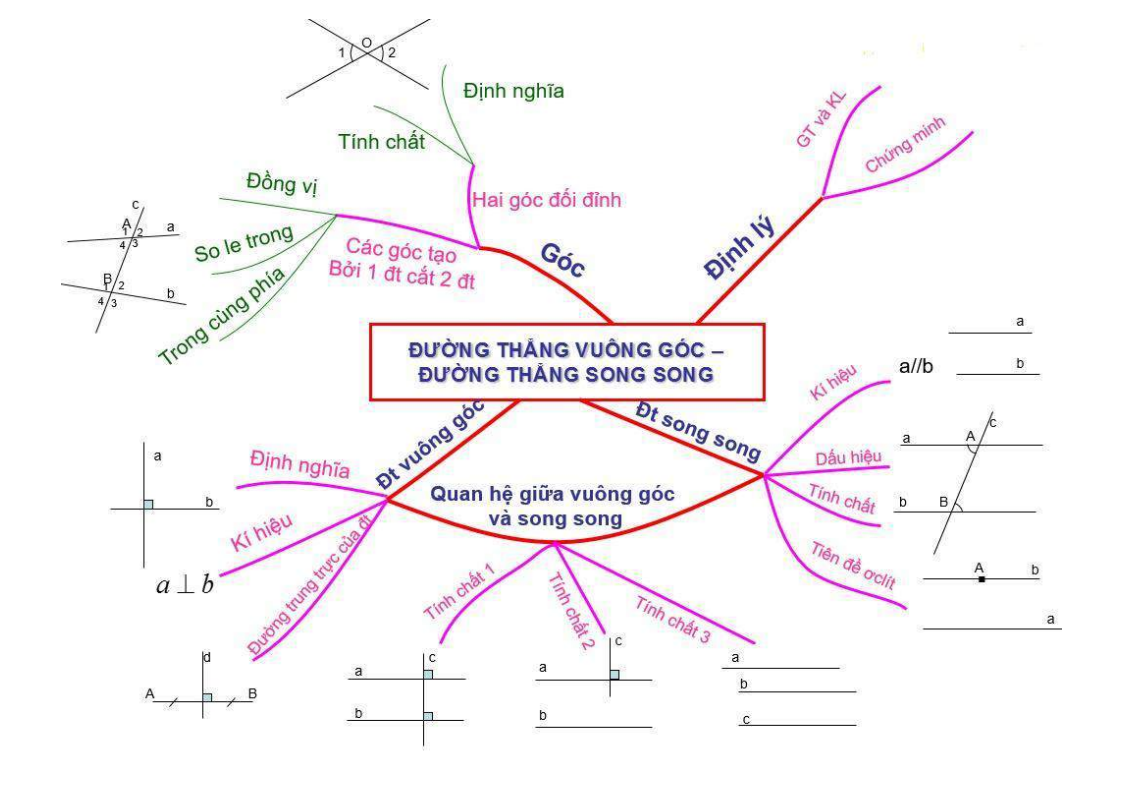
Mọi người giúp mình vẽ sơ đồ tư duy toán hình lớp 7 chương 1 được ko ạ. Làm ơn đi. Mình cần gấp lắm!


a: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}\)
Xét ΔBAM có
MA=MB
Do đó: ΔBAM cân tại M
Xét ΔMAB cân tại M có \(\widehat{MBA}=60^0\)
nên ΔMAB đều
b: ΔMAB đều
mà BH là đường cao
nên H là trung điểm của AM
Xét ΔHMN vuông tại H và ΔHAB vuông tại H có
HA=HM
\(\widehat{HMN}=\widehat{HAB}\)
Do đó: ΔHMN=ΔHAB
=>HN=HB
Xét tứ giác ABMN có
H là trung điểm chung của AM và BN
nên ABMN là hình bình hành
=>AN//MB và AN=MB
AN=MB
MB=MC
Do đó: AN=MC
AN//MB
\(M\in BC\)
Do đó: AN//MC
Xét tứ giác AMCN có
AN//CM
AN=CM
Do đó: AMCN là hình bình hành
Hình bình hành AMCN có AC\(\perp\)MN
nên AMCN là hình thoi
c: ABMN là hình bình hành
=>\(\widehat{NMB}+\widehat{MBA}=180^0\)
=>\(\widehat{NMB}=120^0\)
Hình bình hành ABMN có NB\(\perp\)AM
nên ABMN là hình thoi
Xét ΔNMB có \(\dfrac{NB}{sinNMB}=\dfrac{BM}{sinMNB}\)
=>\(\dfrac{NB}{sin120}=\dfrac{BM}{sin30}\)
=>\(NB=BM\cdot\sqrt{3}\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)
=>\(\dfrac{AC}{2\cdot BM}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(AC=BM\cdot\sqrt{3}\)
=>AC=NB

Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)

Bài 1:
a,b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vừa là đường cao, vừa là phân giác
=>góc BAM=góc CAM và AM vuông góc với BC
c: Xét ΔEBC có
EM vừa là đường cao, vừa là trung tuyến
nên ΔEBC cân tại E
d: Xét ΔKCB có
CE là trung tuyến
CE=KB/2
Do đó: ΔKCB vuông tại C
=>KC//AE

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\)
hay MN//BP và MN=BP
Xét tứ giác BMNP có
MN//BP
MN=BP
Do đó: BMNP là hình bình hành

Thực sự mình cũng không hiểu cách giải theo hướng dẫn bạn trích ở trên. Nhưng bạn có thể như sau:
\(\frac{a}{b^2}+\frac{4b}{a^2+b^2}=\frac{2a}{1-a^2}+\frac{4b}{1-b^2}=\frac{2a^2}{a(1-a^2)}+\frac{4b^2}{b(1-b^2)}\)
Áp dụng BĐT AM-GM:
\(2a^2(1-a^2)^2=2a^2(1-a^2)(1-a^2)\leq \left(\frac{2a^2+1-a^2+1-a^2}{3}\right)^3=\frac{8}{27}\)
$\Rightarrow a(1-a^2)\leq \frac{2}{3\sqrt{3}}$
$\Rightarrow \frac{2a^2}{a(1-a^2)}\geq 3\sqrt{3}a^2$
Tương tự: $\frac{4b^2}{b(1-b^2)}\geq 6\sqrt{3}b^2$
Do đó: $\frac{a}{b^2}+\frac{4b}{a^2+b^2}\geq 3\sqrt{3}(a^2+2b^2)=3\sqrt{3}$ (đpcm)
Bài toán này xuất phát từ bài toán quen thuộc:
Cho $a,b,c>0$ thỏa mãn $a^2+b^2+c^2=1$. CMR:
$\frac{a}{b^2+c^2}+\frac{b}{a^2+c^2}+\frac{c}{a^2+b^2}\geq \frac{3\sqrt{3}}{2}$







a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
=>AEDF là hình chữ nhật
=>AD cắt EF tại trung điểm của mỗi đường
mà I là trung điểm của EF
nên I là trung điểm của AD
=>A,I,D thẳng hàng
b: Xét ΔBAC có DE//AC
nên \(\dfrac{DE}{AC}=\dfrac{BD}{BC}\)
Xét ΔBAC có DF//AB
nên \(\dfrac{DF}{AB}=\dfrac{CD}{CB}\)
\(\dfrac{DE}{AC}+\dfrac{DF}{AB}=\dfrac{BD}{BC}+\dfrac{CD}{BC}=1\)
=>\(\dfrac{DE}{AB}+\dfrac{DF}{AB}=1\)
=>\(DE+DF=AB\)
=>\(2\cdot\left(DE+DF\right)=2AB\)
=>\(C_{AEDF}=2\cdot AB\) không đổi