Sắp xếp các số \(2;\,\frac{5}{{ - 6}}; \frac{3}{5};\, - 1;\,\frac{{ - 2}}{5};\,0\) theo thứ tự tăng dần.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 10 2021
Bài 1:
#include <bits/stdc++.h>
using namespace std;
long long a[100],n,i,j,tam;
int main()
{
cin>>n;
for (i=1; i<=n; i++)
cin>>a[i];
for (i=1; i<=n-1; i++)
for (j=i+1; j<=n; j++)
if (a[i]<a[j]) swap(a[i],a[j]);
for (i=1; i<=n;i++)
cout<<a[i]<<" ";
return 0;
}
23 tháng 3 2019
a) Các số theo thứ tự từ lớn đến bé là: 909; 803; 704; 605; 602; 408; 301; 207; 106
b) Các số theo thứ tự từ bé đến lớn là: 106; 207; 301; 408; 602; 605; 704; 803; 909
Sắp xếp như thế nào tùy vào đơn vị lớn hơn hay bé hơn của chúng.
~Học tốt~
QT
Quoc Tran Anh Le
Giáo viên
13 tháng 9 2023
- Sắp xếp theo thứ tự tăng dần của cột Tốt
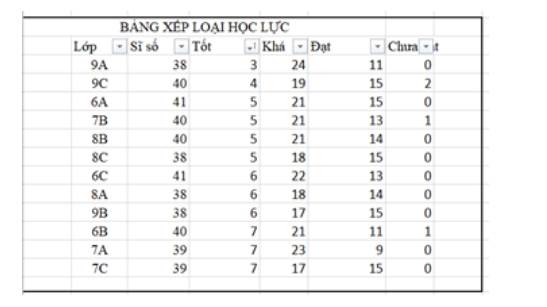
- Sắp xếp theo thứ tự giảm dần của cột Sĩ số
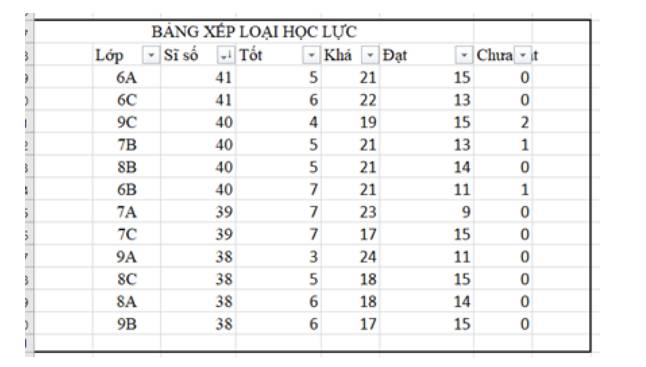
- Kết quả bảng dữ liệu được sắp xếp theo thứ tự trên một cột chính, nếu có nhiều dòng có giá trị khác nhau trên cột chính thì chúng sẽ được sắp xếp theo thứ tự trên cột phụ (khác với cột chính). Ví dụ, trong hoạt động trên, cột Sĩ số được coi là cột chính, cột Tốt là cột phụ. Do đó, cách sắp xếp số lượng học sinh xếp loại tốt của các lớp có cùng sĩ số theo thứ tự tăng dần của cột tốt.
21 tháng 11 2015
2.a) Xếp theo thứ tự tăng dần : -17;-2;0;1;2;5
a) Xếp theo thứ tự giảm dần : 2014;15;7;0;-8;-101;
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
a) Ta có:
\(\begin{array}{l}\frac{{ - 3}}{7} = \frac{{ - 6}}{{14}} ; \frac{{ - 1}}{2}=\frac{{ - 7}}{{14}} ;\\\,\frac{2}{5} = \frac{{14}}{{35}}; \frac{2}{7}=\frac{{10}}{{35}} \end{array}\)
Vì -7 < -6 < 0 nên \(\frac{{ - 7}}{{14}}<\frac{{ - 6}}{{14}}<0\)
Vì 0<10<14 nên \(0<\frac{{10}}{{35}}<\frac{{14}}{{35}}\)
Do đó: \(\frac{{ - 7}}{{14}} < \frac{{ - 6}}{{14}} < \frac{{10}}{{35}} < \frac{{14}}{{35}}\)
=> Sắp xếp các số theo thứ tự tăng dần: \(\frac{{ - 1}}{2};\,\frac{{ - 3}}{7};\,\frac{2}{7};\frac{2}{5}\)
b) Ta có: \(\frac{{ - 5}}{6} = - 0,8\left( 3 \right)\)
Mà \( - 0,75 > - 0,8\left( 3 \right) > - 1 > - 4,5\).
=>Sắp xếp các số theo thứ tự giảm dần: \( - 0,75;\frac{{ - 5}}{6}; - 1; - 4,5\)
TL
19 tháng 8 2023
def nhap_day_so():
"""Hàm nhập dãy số từ bàn phím"""
n = int(input("Nhập số lượng phần tử của dãy: "))
a = []
for i in range(n):
a.append(int(input(f"Nhập phần tử thứ {i+1}: ")))
return a
def sap_xep_chen(a):
"""Hàm sắp xếp dãy số bằng phương pháp sắp xếp chèn"""
for i in range(1, len(a)):
key = a[i]
j = i - 1
while j >= 0 and key < a[j]:
a[j+1] = a[j]
j -= 1
a[j+1] = key
return a
def sap_xep_chon(a):
"""Hàm sắp xếp dãy số bằng phương pháp sắp xếp chọn"""
for i in range(len(a)):
min_idx = i
for j in range(i+1, len(a)):
if a[j] < a[min_idx]:
min_idx = j
a[i], a[min_idx] = a[min_idx], a[i]
return a
def sap_xep_noi_bot(a):
"""Hàm sắp xếp dãy số bằng phương pháp sắp xếp nổi bọt"""
for i in range(len(a)):
for j in range(0, len(a)-i-1):
if a[j] > a[j+1]:
a[j], a[j+1] = a[j+1], a[j]
return a
25 tháng 4 2018
a) Sắp xếp các số nguyên sau theo thứ tự tăng dần:
-17, -2, 0, 1, 2, 5
b) Sắp xếp các số nguyên sau theo thứ tự giảm dần:
2001, 15, 7, 0, -8, -101
Ta có: \(\frac{5}{{ - 6}} = \frac{{ - 5}}{6} = \frac{{ - 5.5}}{{6.5}} = \frac{{ - 25}}{{30}}\)
\(\frac{{ - 2}}{5} = \frac{{ - 2.6}}{{5.6}} = \frac{{ - 12}}{{30}}\)
\( - 1 = \frac{{ - 30}}{{30}}\)
Do \(\frac{{ - 30}}{{30}} < \frac{{ - 25}}{{30}} < \frac{{ - 12}}{{30}}<0\) nên \( - 1 < \frac{5}{{ - 6}} < \frac{{ - 2}}{5}<0\)
Mặt khác, \(0 < \frac{3}{5} < 2\)
Sắp xếp theo thứ tự tăng dần:
\( - 1;\,\frac{5}{{ - 6}};\frac{{ - 2}}{5};\,0; \frac{3}{5}; \,2\).
\(2=\dfrac{120}{60};\dfrac{5}{-6}=\dfrac{-50}{60};\dfrac{3}{5}=\dfrac{36}{60};-1=-\dfrac{60}{60};-\dfrac{2}{5}=-\dfrac{24}{60};0=\dfrac{0}{60}\)
\(-60< -50< -24< 0< 36< 120\)
=>\(-1< -\dfrac{5}{6}< -\dfrac{2}{5}< 0< \dfrac{3}{5}< 2\)