cho tam giác abc dựng phía ngoài các tam giác đều ABE,ACF vẽ hình bình hành AEDF C/m a,GgócBAC=gócBED
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PG
23 tháng 10 2020
Xét tam giác ABD và tam giác FBC có:
AB=FB ( cạnh tam giác đều FAB)
DB=BC ( cạnh tam giác đều DBC)
góc ABD = góc FBC ( cùng bằng góc ABC + 60 độ)
Suy ra tam giác ABD = tam giác FBC (C.G.C)
=> FC=AD
31 tháng 8 2023
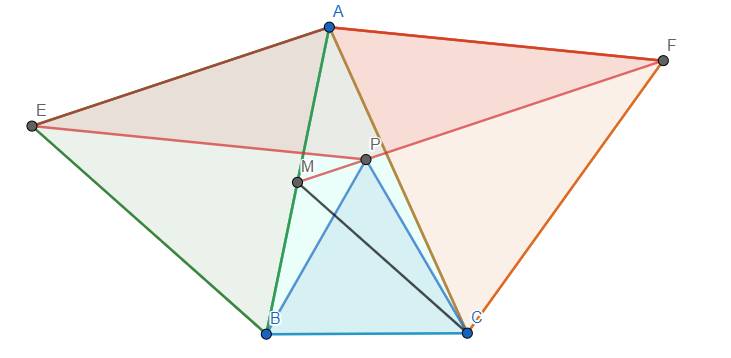
Gọi M là giao điểm của PE với AB.
Ta thấy rằng \(CF=AF=PE,PF=AE=EB\)
Đồng thời \(\widehat{BEP}=60^o-\widehat{AEP}=60^o-\widehat{AFP}=\widehat{PFC}\)
Dẫn đến \(\Delta PBE=\Delta CPF\left(c.g.c\right)\)
\(\Rightarrow PB=PC\) (1)
Mặt khác, \(\widehat{AMF}=\widehat{MAE}=60^o=\widehat{ACF}\) nên tứ giác AMCF nội tiếp.
\(\Rightarrow\widehat{BAC}=\widehat{PFC}\). Mà lại có \(AB=PF,AC=FC\) nên suy ra \(\Delta ABC=\Delta FPC\left(c.g.c\right)\)
\(\Rightarrow PC=BC\) (2)
Từ (1) và (2) \(\Rightarrow\Delta PBC\) đều (đpcm)
DT
12 tháng 2 2022
ta có : góc EBN = góc FCA(1)
lại có : góc EBC = 90 độ ; FCB = 90 độ
=> EBC = FBC (2)
từ (1) và (2) suy ra:
góc PBC = góc PCB
tiếp tục có:
\(\widehat{BPH}+\widehat{CPH}=2.\widehat{EBP}\)
mà \(2.\widehat{EBP}=\widehat{PBC}\)
\(\Rightarrow\widehat{BPH}+\widehat{CPH}=\widehat{PBC}\)
\(mà\widehat{BPH}+\widehat{CPH=}\widehat{BPC}\)
\(\Rightarrow\widehat{PBC}=\widehat{PBC}=\widehat{PCB}\)
từ đó suy ra : tam giác PBC là tam giác đều
( bn không hỉu chỗ nào thì hỏi lại mình nhe)
AH
Akai Haruma
Giáo viên
12 tháng 2 2022
Theo hình vẽ thì $PBC$ làm sao mà là tam giác đều được nhỉ?
