Cho (O,R) đường kính AB. Trên tiếp tuyến Ax lấy AM= R x căn 3, dựng tiếp tuyến MN A. Xác định đường tròn qua 4 điểm: A,M,N,O B. Đường thẳng vuông góc với AB tại O cắt BN tại . Chứng minh OM//BE. C. Các tứ giác BEMO, AMEO, là hình gì D. Tính các góc và diện tích của tứ giác AMEB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 2 2022
a: Xét tứ giác KAOM có
\(\widehat{KAO}+\widehat{KMO}=180^0\)
Do đó: KAOM là tứ giác nội tiếp
b: Xét (O) có
KA là tiếp tuyến
KM là tiếp tuyến
Do đó: KA=KM
hay K nằm trên đường trung trực của AM(1)
Ta có: OA=OM
nên O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra OK là đường trung trực của AM
hay OK\(\perp\)AM
Xét ΔOAK vuông tại A có AI là đường cao
nên \(OI\cdot OK=OA^2\)
CM
8 tháng 6 2017
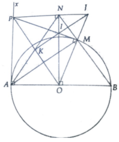
a, HS tự làm
b, Ta có OP ⊥ AM, BM ⊥ AM => BM//OP
c, chứng minh ∆AOP = ∆OBN => OP=BN
lại có BN//OP do đó OPNB là hình bình hành
d, Ta có ON ⊥ PI, PM ⊥ JO mà PM ∩ ON = I => I là trực tâm ∆POJ => JI ⊥ PO(1)
Chứng minh PAON hình chữ nhật => K trung điểm PO
Lại có A P O ^ = O P I ^ = I O P ^ => ∆IPO cân tại I => IKPO (2)
Từ (1),(2) => J,I,K thẳng hàng
14 tháng 3 2021
1: Ta có \(\widehat{KAO}=\widehat{KMO}=90^o\) nên tứ giác KAOM nội tiếp.
2: Theo hệ thức lượng trong tam giác vuông ta có \(OI.OK=OA^2=R^2\)
3: Phần thuận: Dễ thấy H thuộc KI.
Ta có \(\widehat{AHO}=90^o-\widehat{HAI}=\widehat{AMK}=\widehat{AOK}\) nên tam giác AHO cân tại A.
Do đó AH = AO = R.
Suy ra H thuộc (A; R) cố định.
Phần đảo cm tương tự.
Vậy...
LC
29 tháng 5 2017
a) Nối O với N. Ta có \(\widehat{OAN}\)=\(\widehat{OBN}\)=\(\widehat{ONM}\)=90° →các góc này nội tiếp chắn nửa đường tròn đường kính ON →O,A,B,N,M cùng nằm trên đường tròn đường kính ON.
b) Nối A với M. Xét tứ giác nội tiếp OANB(chứng minhnội tiếp trước)ta có \(\widehat{AMO}\)=\(\frac{1}{2}\)\(\widebat{OA}\);\(\widehat{OAB}\)=\(\frac{1}{2}\)\(\widebat{OB}\) mà
- \(\widebat{OA}\)=\(\widebat{OB}\)→\(\widehat{AMO}\)=.\(\widehat{OAB}\)=\(\widehat{OAI}\)Xét tam giác OAI và tam giác OMA: \(\widehat{O}\)chung ,\(\widehat{OAI}\)=\(\widehat{AMO}\)\(\Rightarrow\)hai tam giác đồng dạng (g.g) \(\Rightarrow\)\(\frac{OI}{OA}\)=\(\frac{OA}{OM}\)\(\Leftrightarrow\)OI.OM=\(^{OA^2}\)=Rbình.
- c)
30 tháng 12 2023
a: Xét (O) có
MA,MC là các tiếp tuyến
Do đó: MA=MC
=>\(\widehat{MAC}=\widehat{MCA}\)
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)CB tại C
=>AC\(\perp\)BD tại C
=>ΔACD vuông tại C
Ta có: \(\widehat{MDC}+\widehat{MAC}=90^0\)(ΔACD vuông tại C)
\(\widehat{MCD}+\widehat{MCA}=\widehat{DCA}=90^0\)
mà \(\widehat{MAC}=\widehat{MCA}\)
nên \(\widehat{MDC}=\widehat{MCD}\)
=>MC=MD
mà MC=MA
nên MA=MD
=>M là trung điểm của AD
b: Xét (O) có
MC,MA là các tiếp tuyến
Do đó: OM là phân giác của góc AOC
=>\(\widehat{AOC}=2\cdot\widehat{MOC}\)
Ta có: tia OC nằm giữa hai tia OM và ON
=>\(\widehat{MOC}+\widehat{NOC}=\widehat{MON}=90^0\)
=>\(\widehat{NOC}=90^0-\widehat{MOC}\)
Ta có: \(\widehat{COA}+\widehat{COB}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{COM}+\widehat{COB}=2\cdot90^0=2\cdot\widehat{COM}+2\cdot\widehat{CON}\)
=>\(\widehat{COB}=2\cdot\widehat{CON}\)
=>ON là phân giác của góc COB
Xét ΔOBN và ΔOCN có
OB=OC
\(\widehat{BON}=\widehat{CON}\)
ON chung
Do đó: ΔOBN=ΔOCN
=>\(\widehat{OBN}=\widehat{OCN}=90^0\)
=>NB là tiếp tuyến của (O)
a: Xét tứ giác MAON có \(\widehat{MAO}+\widehat{MNO}=90^0+90^0=180^0\)
nên MAON là tứ giác nội tiếp đường tròn đường kính MO
=>ĐƯờng tròn đi qua bốn điểm A,M,N,O là đường tròn đường kính MO
b: Xét (O) có
MA,MN là tiếp tuyến
Do đó: MA=MN
=>M nằm trên đường trung trực của AN(1)
OA=ON
=>O nằm trên đường trung trực của AN(2)
Từ (1) và (2) suy ra OM là đường trung trực của AN
=>OM\(\perp\)AN(3)
Xét (O) có
ΔANB nội tiếp
AB là đường kính
Do đó: ΔANB vuông tại N
=>AN\(\perp\)NB
=>AN\(\perp\)BE(4)
Từ (3) và (4) suy ra OM//BE
c: Xét ΔMAO vuông tại A và ΔEOB vuông tại O có
OA=OB
\(\widehat{MOA}=\widehat{EBO}\)(hai góc đồng vị, MO//EB)
Do đó: ΔMAO=ΔEOB
=>MO=EB
Xét tứ giác BOME có
OM//BE
OM=BE
Do đó: BOME là hình bình hành
=>OB//EM và OB=ME
OB//ME
A\(\in\)OB
Do đó: OA//ME
OA=OB
OB=ME
Do đó: OA=ME
Xét tứ giác AOEM có
AO//EM
AO=EM
Do đó: AOEM là hình bình hành
Hình bình hành AOEM có \(\widehat{MAO}=90^0\)
nên AOEM là hình chữ nhật
d: ΔMAO vuông tại A
=>\(MA^2+OA^2=MO^2\)
=>\(MO^2=R^2+\left(R\sqrt{3}\right)^2=4R^2\)
=>MO=2R
=>EB=2R
Xét ΔEOB vuông tại O có \(cosB=\dfrac{BO}{EB}=\dfrac{1}{2}\)
nên góc B=60 độ
ME//AB
=>\(\widehat{MEB}+\widehat{B}=180^0\)
=>\(\widehat{MEB}=180^0-60^0=120^0\)
AOEM là hình chữ nhật
=>\(\widehat{EMA}=\widehat{MAO}=90^0\)
=>\(\widehat{EMA}=\widehat{MAB}=90^0\)
Diện tích tứ giác AEMB là:
\(S_{AEMB}=\dfrac{1}{2}\left(ME+AB\right)\cdot AM=\dfrac{1}{2}\cdot R\sqrt{3}\left(R+2R\right)=\dfrac{R\sqrt{3}}{2}\cdot3R=3\sqrt{3}\cdot\dfrac{R^2}{2}\)