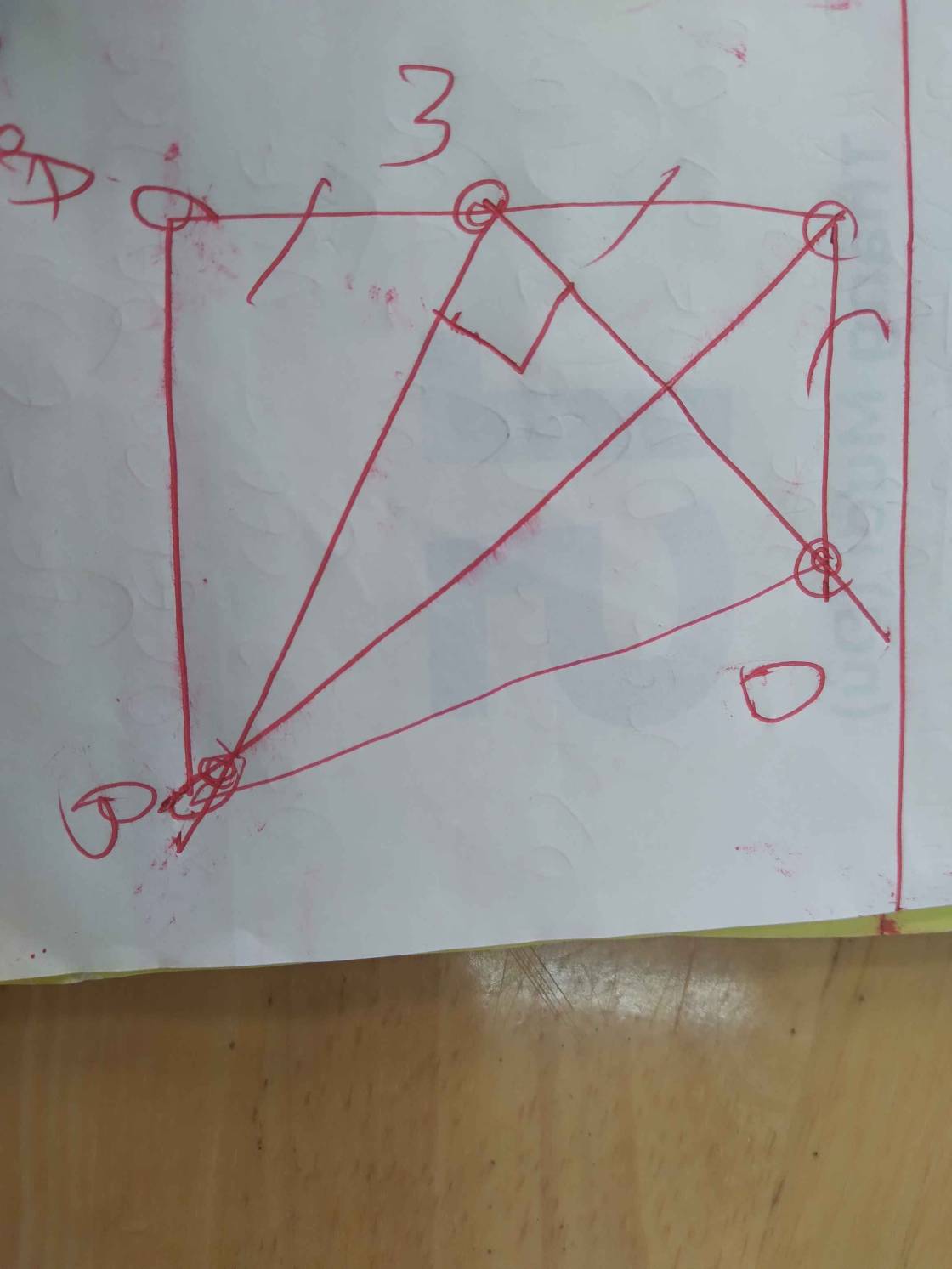
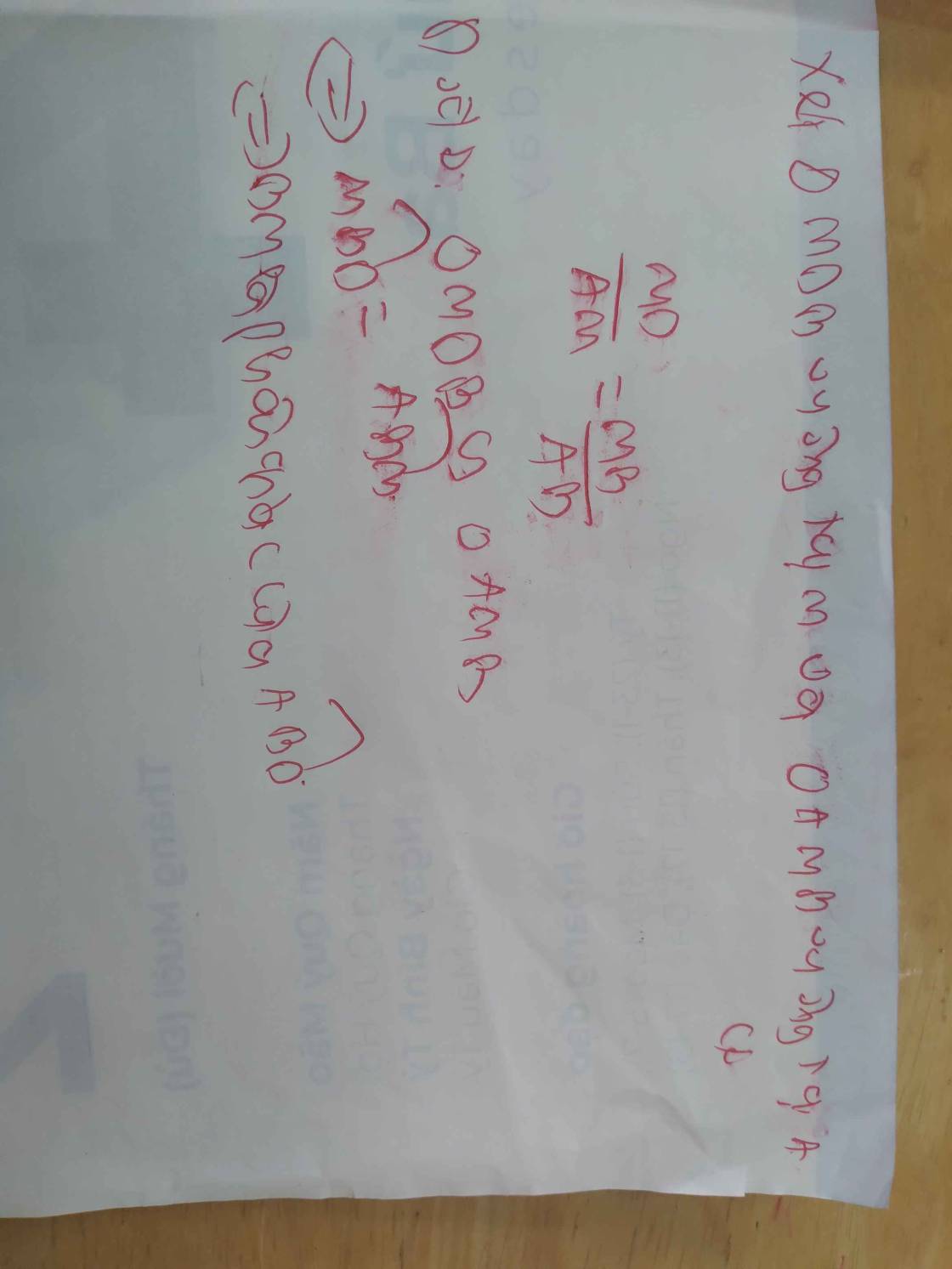Tam giác ABC vuông cân tại A ,M là 1 điểm trên AC ,I là trung điểm của BM ,N là trung điểm của AC .Đường thẳng đi qua A và vuông góc với IN căt đường thẳng đi qua C và vuông góc với AC tại E .chứng mi...

NX

Nguyễn Xuân Dũng

20 tháng 7 2017 - olm

Tam giác ABC vuông cân tại A ,M là 1 điểm trên AC ,I là trung điểm của BM ,N là trung điểm của AC .Đường thẳng đi qua A và vuông góc với IN căt đường thẳng đi qua C và vuông góc với AC tại E .chứng minh IN=1/2 AEtam giác ABC vuông cân tại A ,M là 1 điểm trên AC ,I là trung điểm của BM ,N là trung điểm của AC .Đường thẳng đi qua A và vuông góc với IN căt đường thẳng đi qua C và vuông góc với AC...

Đọc tiếp

#Toán lớp 8

0

NL

Nguyễn Linh Chi

17 tháng 8 2016 - olm

cho tam giác ABC vuông cân tại A, P là trung điểm của AB. trên AB lấy M gọi M là trung điểm của MC. E là giao điểm của đường thẳng đi qua B song song với AC và đường thẳng đi qua A vuông góc vs PN CMR: Tam giác BME vuông cân

#Toán lớp 7

0

BN

Bùi Nguyệt Nhi

6 tháng 4 2017 - olm

1)cho tam giác ABC vuông cân tại A. M là trung điểm của BC. G thuộc AB sao cgo AG=\(\frac{1}{3}\)AB, E là chân đường vuông góc hạ từ M xuống CG. MG và AC cắt nhau tại D. so sánh DE và BC2) cho tam giác ABC vuông tại A và \(\widehat{BAC}\)= 60' , M thuộc BC sao cho AB+BM=AC+CM. tính\(\widehat{CAM}\)3) cho tam giác ABC cân tại A , gọi E là điểm bất kì nằm giữa B và C , đường thẳng qua E vuông góc với AB và đường thẳng...

Đọc tiếp

#Toán lớp 7

0

DT

Đào Trọng Luân

18 tháng 12 2017 - olm

Cho tam giác ABC cân tại A. Trên đường thẳng vuông góc với AC tại A lấy điểm D [B và D nằm khác mặt phẳng đối với AC]. Đường thẳng vuông góc với AB tại B và đường thẳng đi qua trung điểm M của của CD vuông góc với AD tại E cắt nhau tại K.

Chứng minh tam giác KBD cân bằng hai cách

#Toán lớp 7

0

M

maithuyentk

28 tháng 3 2020 - olm

Bài1:Cho tam giác ABC,M là điểm nằm trong tam giác. Gọi D là giao điểm của AM và BC, E là giao điểm của BM và CA. F là giao điểm của CM và AB, đường thẳng đi qua M và song song với BC cắt DE, DF lần lượt tại K và I. Cmr MI=MK.Bài 2:Cho tam giác ABC, các đường trung tuyến BM, CN cắt nhau tại G, K là điểm trên cạnh BC, đường thẳng đi qua K và song song CN cắt AB ở D, đường thẳng đi qua K và song song với...

Đọc tiếp

#Toán lớp 8

0

NA

Nguyễn Anh Bắc

20 tháng 1 2021

tam giác ABC cân tại A, đường thẳng đi qua B vuông góc AB cắt đường thẳng đi qua C vuông AC tại H. AH cắt BC tại I. M là trung điểm BI. Từ I kẻ đường thẳng song song với AB cắt AC tại N. Chứng minh tam giác MNH vuông

#Toán lớp 7

0

VT

Võ Thư Quỳnh

19 tháng 4 2017 - olm

cho tam giác ABC vuông cân tại A, M là 1 điểm thuộc cạnh AC. Gọi I,K lần lượt là trung điểm của canh BM,AC. Qua A kẻ đường thẳng vuông góc với IK, qua C kẻ đường thẳng vuông góc với AC, chúng cắt nhau tại H. Tính góc HMC

#Toán lớp 7

1

KN

Kiệt Nguyễn

16 tháng 3 2020

Kẻ \(BN\perp AH\left(N\in AC\right)\)

Khi đó \(BN//IK\)(cùng vuông góc với AH)

Kết hợp với I là trung điểm của BM suy ra IK là đường trung bình của \(\Delta MBC\)

\(\Rightarrow\)K là trung điểm của MN

hay MK = NK kết hợp giả thiết AK = CK suy ra AN = CM (cộng theo vế) (1)

Xét \(\Delta ABN\)và \(\Delta CAH\)có:

AB = CA (gt)

\(\widehat{ABN}=\widehat{CAH}\)(cùng phụ với \(\widehat{BAH}\))

Do đó \(\Delta ABN=\Delta CAH\left(cgv-gnk\right)\)

\(\Rightarrow AN=CH\)(hai cạnh tương ứng) (2)

Từ (1) và (2) suy ra CH = CM

Mà \(\widehat{HCM}=90^0\)suy ra \(\Delta HCM\)vuông cân tại C

Vậy \(\widehat{HMC}=45^0\)

Đúng(0)

NA

Nguyễn Anh Kim Hân

27 tháng 11 2018 - olm

Cho tam giác ABC vuông tại A,AB < AC,M là trung điểm của AC. Đường thẳng qua M vuông góc với BC và đường thẳng qua C vuông góc với AC cắt nhau tại D. Chứng minh rằng AD vuông góc với BM.

#Toán lớp 8

0

BC

Big City Boy

2 tháng 3 2021

Cho tam giác nhọn ABC có AB<AC, các đường cao AD, BE, CF cắt nhau tại H. ĐƯờng thẳng đi qua C và vuông góc với AC cắt đường thẳng đi qua B và vuông góc với AB tại điểm K. Gọi M là trung điểm của BC, I là trung điểm của AKa) CHứng minh: BE<CF và \(IM=\dfrac{1}{2}AH\)b) Gọi G là trọng tâm của tam giác ABC. CHứng minh: 3 điểm H, G, I thẳng hàng. c)...

Đọc tiếp

#Toán lớp 8

1

HN

Hồng Nhan

3 tháng 3 2021

a) Ta có:

\(\left\{{}\begin{matrix}BH\perp AC\\KC\perp AC\end{matrix}\right.\) ⇒ \(BH\text{//}KC\)

\(\left\{{}\begin{matrix}CH\perp AB\\BK\perp AB\end{matrix}\right.\) ⇒ \(CH\text{//}BK\)

\(Xét\) \(tứ\) \(giác\) \(BKCH\) \(có:\) \(\left\{{}\begin{matrix}BH\text{//}KC\\CH\text{//}BK\end{matrix}\right.\)

⇒ Tứ giác \(BKCH\) là hình hình hành. Mà M là trung điểm của đường chéo BC

⇒ \(\left\{{}\begin{matrix}H,M,K_{ }thẳng_{ }hàng\\HM=MK\end{matrix}\right.\)

Xét \(\Delta AHK\) có: \(\left\{{}\begin{matrix}AI=IK\left(gt\right)\\HM=MK\left(cmt\right)\end{matrix}\right.\)

⇒ \(IM\) là đường trung bình của \(\Delta AHK\)

⇒ \(IM=\dfrac{1}{2}AH\) \(\left(ĐPCM\right)\)

c)

Ta có:

\(\dfrac{S_{\Delta HBC}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HD.BC}{\dfrac{1}{2}.AD.BC}=\dfrac{HD}{AD}\)

\(\dfrac{S_{\Delta HAC}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HE.AC}{\dfrac{1}{2}.BE.AC}=\dfrac{HE}{BE}\)

\(\dfrac{S_{\Delta HBA}}{S_{\Delta ABC}}=\dfrac{\dfrac{1}{2}.HF.AB}{\dfrac{1}{2}.CF.AB}=\dfrac{HF}{CF}\)

⇒ \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=\dfrac{S_{\Delta HBC}+S_{\Delta HAC}+S_{\Delta HAB}}{S_{\Delta ABC}}=\dfrac{S_{\Delta ABC}}{S_{\Delta ABC}}\)

⇔ \(\dfrac{HD}{AD}+\dfrac{HE}{BE}+\dfrac{HF}{CF}=1\) \(\left(ĐPCM\right)\)

Đúng(3)

JN

Jess Nguyen

16 tháng 3 2022

Cho tam giác ABC vuông tại A, AC = 8cm. Gọi M là trung điểm của AC. Đường thẳng qua M, vuông góc với BM và đường thẳng qua C, vuông góc với AC cắt nhau tại D.

a) Chứng minh tam giác ABM và tam giác CMD đồng dạng.

b) Tính trị số của tích AB.CD.

c) Chứng minh BM là tia phân giác của góc ABD

#Toán lớp 8

1