Xét đường tròn đường kính AB=4 và một điểm M di chuyển trên đoạn AB, đặt AM=x (H.6.19). Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) là diện tích phần hình phằng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của x để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ.
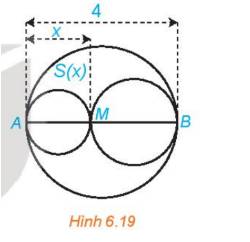




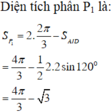
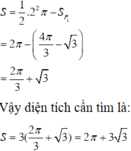
Ta có: AM<AB nên \(0 < x < 4\)
Diện tích hình tròn đường kính AB là \({S_0} = \pi .{\left( {\frac{{AB}}{2}} \right)^2} = 4\pi \)
Diện tích hình tròn đường kính AM là \({S_1} = \pi .{\left( {\frac{{AM}}{2}} \right)^2} = \frac{{\pi .{x^2}}}{4}\)
Diện tích hình tròn đường kính MB là \({S_2} = \pi .{\left( {\frac{{MB}}{2}} \right)^2} = \pi .\frac{{{{\left( {4 - x} \right)}^2}}}{4}\)
Diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ là \(S(x) = {S_0} - {S_1} - {S_2} = 4\pi - \frac{{{x^2}}}{4}\pi - \frac{{{{\left( {4 - x} \right)}^2}}}{4}\pi = \frac{{ - {x^2} + 4x}}{2}\pi \)
Vì diện tich S(x) không vượt quá 1 nửa tổng diện tích hai hình tròn nhỏ nên:
\(S(x) \le \frac{1}{2}\left( {{S_1} + {S_2}} \right)\)
Khi đó : \(\frac{{ - {x^2} + 4x}}{2}\pi \le \frac{1}{2}.\frac{{{x^2} - 4x + 8}}{2}\pi \)
\( \Leftrightarrow - {x^2} + 4x \le \frac{{{x^2} - 4x + 8}}{2}\)
\( \Leftrightarrow - 2{x^2} + 8x \le {x^2} - 4x + 8\)
\( \Leftrightarrow 3{x^2} - 12x + 8 \ge 0\)
Xét tam thức \(3{x^2} - 12x + 8\) có \(\Delta ' = 12 > 0\) nên f(x) có 2 nghiệm phân biệt \({x_1} = \frac{{6 - 2\sqrt 3 }}{3};{x_2} = \frac{{6 + 2\sqrt 3 }}{3}\)
Mặt khác a=3>0, do đó ta có bảng xét dấu:
Do đó \(f(x) \ge 0\) với mọi \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)
Mà 0<x<4 nên \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)