Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi bàn kính hình tròn nhỏ là a
=> Bán kính hình tròn lớn là 2a
Ta có
Diện tích hình tròn nhỏ là
\(a^2.3,14\)
Diện tích hình tròn lớn là
\(\left(3a\right)^2.3,14=9a^2.3,14\)
Dễ thấy \(\frac{9a^2.3,14}{a^2.3,14}=9\)
=> Diện tích hình tròn lớn gấp 9 lần diên tích hình tròn nhỏ

a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
nên ABOC là tứ giác nội tiếp(1)
b: Xét tứ giác OEAC có
\(\widehat{OEA}+\widehat{OCA}=180^0\)
Do đó: OEAC là tứ giác nội tiếp(2)
Từ (1) và (2) suy ra O,E,B,A,C cùng thuộc một đường tròn
c: \(\widehat{BIC}=\dfrac{sđ\stackrel\frown{BC}}{2}=\dfrac{\widehat{BOC}}{2}\)
mà \(\widehat{AOC}=\dfrac{\widehat{BOC}}{2}\)
nên \(\widehat{BIC}=\widehat{AOC}\)

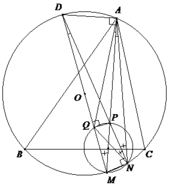
2) Tứ giác APQD nội tiếp ( P Q D ^ = M A D ^ = 90 0 ),
suy ra P A Q ^ = P D Q ^ = N D M ^ (3).
Xét (O), ta có N D M ^ = N A M ^ (4).
Từ (3) và (4) P A Q ^ = N A P ^ , suy ra AP là phân giác của góc N A Q ^ (*).
Xét (O), ta có A N D ^ = A M D ^ .
Xét đường tròn đường kính MP có Q M P ^ = Q N P ^ ⇒ A N P ^ = Q N P ^ , nên NP là phân giác của góc ANQ (**).
Từ (*) và (**), suy ra P là tâm đường tròn nội tiếp tam giác ANQ

a) Xét tứ giác BEDC có:
∠BEC = 90o (CE là đường cao)
∠BDC = 90o (BD là đường cao)
=> Hai đỉnh D và E cùng nhìn cạnh BC dưới 1 góc vuông
=> Tứ giác BEDC là tứ giác nội tiếp
b) Xét ΔAEC và ΔADB có:
∠BAC là góc chung
∠AEC = ∠BDA = 90o
=> ΔAEC ∼ ΔADB (g.g)
\(\Rightarrow\frac{AE}{AD}=\frac{AC}{AB}\Rightarrow\text{AE.AB = AC.AD}\)
c) Ta có:
∠FBA = 90o (góc nội tiếp chắn nửa đường tròn)
=>FB⊥AB
Lại có: CH⊥AB (CH là đường cao)
=> CH // FB
Tương tự,( FCA) = 90o (góc nội tiếp chắn nửa đường tròn)
=>FC⊥AC
BH là đường cao => BH ⊥AC
=> FC // BH
Xét tứ giác CFBH có:
CH // FB
FC // BH
=> Tứ giác CFBH là hình bình hành.
Mà I là trung điểm của BC
=> I cũng là trung điểm của FH
Hay F, I, H thẳng hàng.
2) Diện tích xung quanh của hình trụ:
S = 2πRh = 2πR2 = 128π (do chiều cao bằng bán kính đáy)
=> R = 8 cm ; h = 8cm
Thể tích của hình trụ là
V = πR2 h = π.82.8 = 512π (cm3)
HÌNH TRONG THỐNG KÊ HỎI ĐÁP NHA VỚI LẠI MIK TRẢ LỜI TOÀN CÂU KHÓ MÀ CHẲNG CÓ CÁI GP NÀO
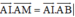 và
và 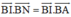
 theo R.
theo R.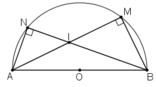
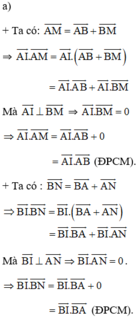


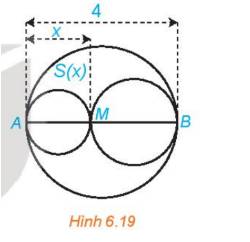
Ta có: AM<AB nên \(0 < x < 4\)
Diện tích hình tròn đường kính AB là \({S_0} = \pi .{\left( {\frac{{AB}}{2}} \right)^2} = 4\pi \)
Diện tích hình tròn đường kính AM là \({S_1} = \pi .{\left( {\frac{{AM}}{2}} \right)^2} = \frac{{\pi .{x^2}}}{4}\)
Diện tích hình tròn đường kính MB là \({S_2} = \pi .{\left( {\frac{{MB}}{2}} \right)^2} = \pi .\frac{{{{\left( {4 - x} \right)}^2}}}{4}\)
Diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ là \(S(x) = {S_0} - {S_1} - {S_2} = 4\pi - \frac{{{x^2}}}{4}\pi - \frac{{{{\left( {4 - x} \right)}^2}}}{4}\pi = \frac{{ - {x^2} + 4x}}{2}\pi \)
Vì diện tich S(x) không vượt quá 1 nửa tổng diện tích hai hình tròn nhỏ nên:
\(S(x) \le \frac{1}{2}\left( {{S_1} + {S_2}} \right)\)
Khi đó : \(\frac{{ - {x^2} + 4x}}{2}\pi \le \frac{1}{2}.\frac{{{x^2} - 4x + 8}}{2}\pi \)
\( \Leftrightarrow - {x^2} + 4x \le \frac{{{x^2} - 4x + 8}}{2}\)
\( \Leftrightarrow - 2{x^2} + 8x \le {x^2} - 4x + 8\)
\( \Leftrightarrow 3{x^2} - 12x + 8 \ge 0\)
Xét tam thức \(3{x^2} - 12x + 8\) có \(\Delta ' = 12 > 0\) nên f(x) có 2 nghiệm phân biệt \({x_1} = \frac{{6 - 2\sqrt 3 }}{3};{x_2} = \frac{{6 + 2\sqrt 3 }}{3}\)
Mặt khác a=3>0, do đó ta có bảng xét dấu:
Do đó \(f(x) \ge 0\) với mọi \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)
Mà 0<x<4 nên \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)