Cho hai số x,y thỏa mãn xy+x+y=−1 và x^2 y + xy^ 2 = − 12 .Giá trị biểu thức A = x^3 + y^3 bằng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
YY
0

SH
Cho hai số dương x,y thỏa mãn: 2x2+xy-y2=0. Tính giá trị biểu thức:
A = \(\frac{x^2y+xy^2}{x^3+y^3}\)
0


25 tháng 12 2021
\(Q=x^2+y^2=\left(x+y\right)^2-2xy=\left(-1\right)^2-2\left(-6\right)=13\\ P=x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)\\ P=\left(-1\right)^3-3\left(-6\right)\left(-1\right)=-1-18=-19\)
25 tháng 12 2021
\(P=\left(x+y\right)^2-2xy=\left(-1\right)^2-2\cdot\left(-6\right)=1+12=13\)
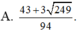
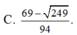
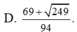
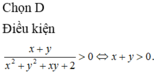





Lời giải:
Đặt $xy=a; x+y=b$ thì theo đề ta có:
$a+b=-1$ và $ab=-12$
Ta cần tính: $A=(x+y)^3-3xy(x+y)=b^3-3ab=b^3-3(-12)=b^3+36$
Từ $a+b=-1\Rightarrow a=-b-1$. Thay vào $ab=-12$
$\Rightarrow (-b-1)b=-12$
$\Leftrightarrow (b+1)b=12$
$\Leftrightarrow b^2+b-12=0$
$\Leftrightarrow (b-3)(b+4)=0$
$\Leftrightarrow b=3$ hoặc $b=-4$
Nếu $b=3$ thì $A=3^3+36=63$
Nếu $b=-4$ thì $A=(-4)^3+36=-28$