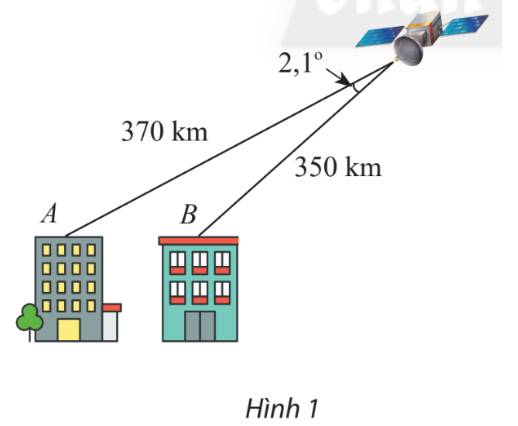
Tính khoảng cách AB giữa hai nóc tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 370 km, 350 km và góc nhìn từ vệ tinh đến A và B là \(2,{1^ \circ }.\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì hai vệ tinh cùng cách mặt đất 230 km nên tam giác AOB cân tại O.
Ta có: OA = R + 230
= 6370 + 230 = 6600 (km)
Trong tam giác AOB ta có: OH ⊥ AB
Suy ra: HA = HB = AB/2 = 2200/2 = 1100 (km)
Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:
O A 2 = A H 2 + O H 2
Suy ra: O H 2 = O A 2 - A H 2
Suy ra:
OH = ![]() ≈ 6508 (km)
≈ 6508 (km)
Vì OH > R nên hai vệ tinh nhìn thấy nhau.

Chọn D.
Tại độ cao h, lực hấp dẫn đóng vai trò là lực hướng tâm: Fhd = Fht
Vì ở độ cao h, vệ tinh có trọng lượng 920 N nên Fhd = 920 N
Mặt khác:
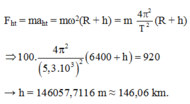

Chọn D.
Tại độ cao h, lực hấp dẫn đóng vai trò là lực hướng tâm:
F h d = F h t
Vì ở độ cao h, vệ tinh có trọng lượng 920 N nên
F h d = 920 N
Mặt khác:
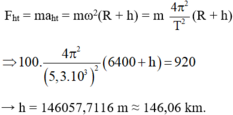

Tam giác ABC vuông tại B nên ta có: \(\tan C = \frac{{AB}}{{CB}} \Leftrightarrow AB = \tan {32^ \circ }.(1 + x)\)
Tam giác ADB vuông tại B nên ta có: \(\tan D = \frac{{AB}}{{DB}} \Leftrightarrow AB = \tan {40^ \circ }.x\)
\(\begin{array}{l} \Rightarrow \tan {32^ \circ }.(1 + x) = \tan {40^ \circ }.x\\ \Leftrightarrow x.(\tan {40^ \circ } - \tan {32^ \circ }) = \tan {32^ \circ }\\ \Leftrightarrow x = \frac{{\tan {{32}^ \circ }}}{{\tan {{40}^ \circ } - \tan {{32}^ \circ }}}\\ \Leftrightarrow x \approx 2,9\;(km)\end{array}\)
\( \Rightarrow AB \approx \tan {40^ \circ }.2,92 \approx 2,45\;(km)\)
Vậy chiều cao của ngọn núi là 2,45 km.
Áp dụng định lí cosin, ta có:
\(\begin{array}{l}A{B^2} = {370^2} + {350^2} - 2.370.350.\cos 2,{1^ \circ }\\ \Rightarrow AB \approx 23,96\;(km)\end{array}\)
Vậy khoảng cách giữa hai tòa nhà là 23,96 km.