Một con tàu chuyển động từ bờ bên này sang bờ bên kia của một dòng sông với vận tốc riêng không đổi. Giả sử vận tốc dòng nước là không đổi và đáng kể, các yếu tố bên ngoài khác không ảnh hưởng đến vận tốc thực tế của tàu. Nếu không quan tâm đến điểm đến thì cần giữ lái cho tàu tạo với bờ sông một góc bao nhiêu để tàu sang bờ bên kia được nhanh...
Đọc tiếp
Một con tàu chuyển động từ bờ bên này sang bờ bên kia của một dòng sông với vận tốc riêng không đổi. Giả sử vận tốc dòng nước là không đổi và đáng kể, các yếu tố bên ngoài khác không ảnh hưởng đến vận tốc thực tế của tàu. Nếu không quan tâm đến điểm đến thì cần giữ lái cho tàu tạo với bờ sông một góc bao nhiêu để tàu sang bờ bên kia được nhanh nhất?
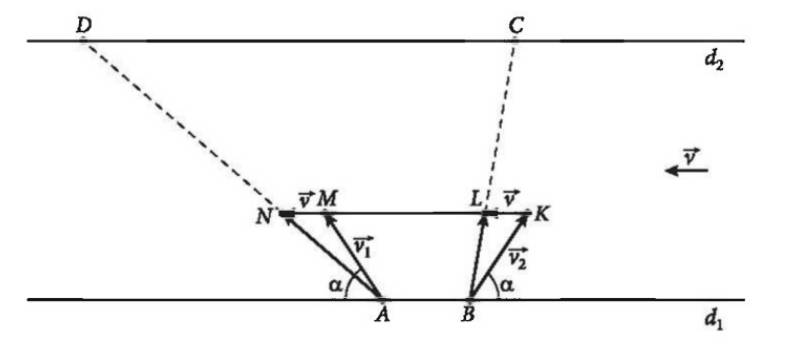
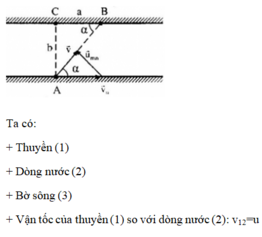
Gọi: vận tốc thực tế của tàu là \(\overrightarrow v \)
Vận tốc riêng của tàu (đối với dòng nước) là \(\overrightarrow {{v_t}} \)
Vận tốc của dòng nước (đối với bờ) là \(\overrightarrow {{v_n}} \)
Ta có: \(\overrightarrow v = \overrightarrow {{v_n}} + \overrightarrow {{v_t}} \)
Để tàu sang bờ bên kia nhanh nhất thì vận tốc thực tế của tàu có hướng vuông góc với bờ.
Theo quy tắc hình bình hành thì \(\overrightarrow v \) là vecto đường chéo xuất phát từ gốc chung của vecto vận tốc riêng của tàu và vecto vận tốc dòng nước tác động lên tàu.