Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Theo đề ta có:
\(v_{23}=v^0\)
\(v_{13}=\sqrt{a^2+b^2}\)
\(\Leftrightarrow v_{13}=v_{12}+v_{23}\)
\(\Rightarrow v_{12}=\sqrt{a^2+b^2}-v^0\)
Vì \(v^0\) không đổi
Để \(v_{12}\) min thì \(\sqrt{a^2+b^2}\) min
\(\Leftrightarrow \) \(a^2+b^2\) min
Mà \(a^2+b^2\) \(\geq 2\) \(\sqrt{ab}\)
Dấu ''='' xảy ra khi
\(a=b\)
Vậy: \(v_{12}=a\sqrt{2}-v^0\)
\(\Leftrightarrow \)

Đáp án D.
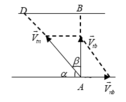
Trong cùng thời gian nước di chuyển được đoạn DB, thuyền di chuyển được đoạn AD. Do v t n = 3 v n b nên AD=3DB. Từ đó suy ra sin β = 1 / 3 hay α ≈ 71 0 C

Đáp án C.
Lúc này theo hình vẽ ta có:
v t b = v t n 2 + v n b 2 = 10 m / s

Đáp án C.
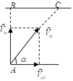
Lúc này theo hình vẽ ta có: v t b = v t n 2 + v n b 2 = 10 m / s

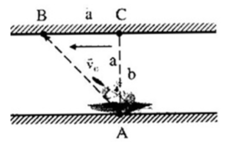


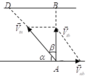
Đáp án B