Question

[Quoc Tran Anh Le]

Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S và từ vị trí S đến vị trí C trên cù lao như Hình 38. Tiền công thiết kế mỗi ki-lô-mét đường dây từ A đến S và từ S đến C lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.

Answer 1

[Hà Quang Minh]

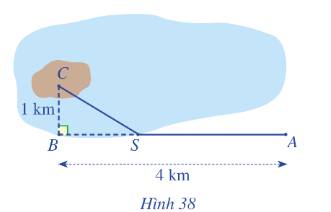
Gọi khoảng cách từ A đến S là x (km) (0<x<4)

\( \Rightarrow BS = 4 - x\)(km)

\( \Rightarrow CS = \sqrt {C{B^2} + B{S^2}} \)\( = \sqrt {1 + \left( {4 - {x^2}} \right)} \)(km)

Tổng số tiền từ A đến C là:

\(3.SA + 5.SC = 3.x + 5.\sqrt {1 + {{\left( {4 - x} \right)}^2}} \)(triệu đồng)

Khi đó ta có phương trình:

\(3.x + 5.\sqrt {1 + {{\left( {4 - x} \right)}^2}}  = 16\)

\( \Leftrightarrow 5\sqrt {1 + {{\left( {4 - x} \right)}^2}}  = 16 - 3x\)

\(\begin{array}{l}25.\left( {{x^2} - 8x + 17} \right) = {\left( {16 - 3x} \right)^2}\\ \Leftrightarrow 25{x^2} - 200x + 425 = 256 - 96x + 9{x^2}\\ \Leftrightarrow 16{x^2} - 104x + 169 = 0\\ \Leftrightarrow x = \frac{{13}}{4}\left( {tm} \right)\end{array}\)

Do \(16 - 3x > 0 \Leftrightarrow \forall 0 < x < 4\)

=> \(SC = \sqrt {1 + \left( {4 - {x^2}} \right)}  = 1,25\)

Vậy tổng ki-lô-mét đường dây điện đã thiết kế là SA+SC=3,25+1,25=4,5 (km)