Từ điểm A ở ngoài đường tròn [O;R] vẽ hai tiếp tuyến AB;AC với đường tròn [B,C là tiếp điểm ]. Gọi H là chân đường vuông góc kẻ từ B đến đường kính CD.a cm 4 điểm A,B,C,O cùng thuộc 1 đường trònb cm BD //OAc i là giao điểm BH và AD. Cm i là trung điểm bhGiúp em phần c với...
Đọc tiếp
Từ điểm A ở ngoài đường tròn [O;R] vẽ hai tiếp tuyến AB;AC với đường tròn [B,C là tiếp điểm ]. Gọi H là chân đường vuông góc kẻ từ B đến đường kính CD.
a cm 4 điểm A,B,C,O cùng thuộc 1 đường tròn
b cm BD //OA
c i là giao điểm BH và AD. Cm i là trung điểm bh
Giúp em phần c với ạ!
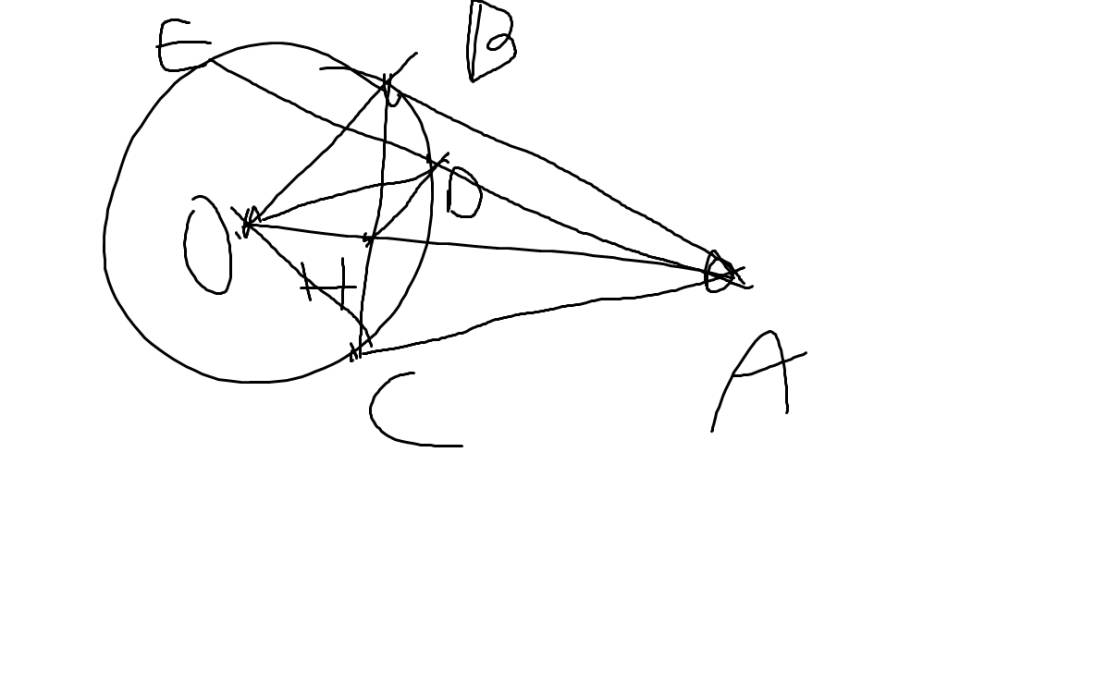
c: IH vuông góc CD
AC vuông góc CD
DO đó: IH//AC
Xét ΔDCA có IH//AC
nên \(\dfrac{IH}{AC}=\dfrac{DH}{DC}\)
=>\(IH=\dfrac{AC\cdot DH}{DC}\)
Xét ΔACO vuông tại C và ΔBHD vuông tại H có
\(\widehat{AOC}=\widehat{BDH}\left(=\widehat{AOB}\right)\)
Do đó: ΔACO đồng dạng với ΔBHD
=>\(\dfrac{AC}{BH}=\dfrac{CO}{HD}\)
=>\(BH=\dfrac{AC\cdot HD}{CO}\)
\(\dfrac{BH}{IH}=\dfrac{DO}{OC}=2\)
=>BH=2IH
=>I là trung điểm của BH