Cho tam giác ABC vuông tại A có góc B=60độ. Cạnh BC=2a. Hãy tính tỉ số lượng giác của góc 30độ và góc 60độ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
cho tam giác ABC vuông tại A . Số đo góc B = 60 độ thì số đo góc C bằng:A.45độ B.60độ C.30độ D.120độ

Vì \(\Delta ABC^vA\Rightarrow\widehat{C}+\widehat{B}=90^0\Rightarrow\widehat{C}=90^0-60^0=30^0\)
Đáp án C

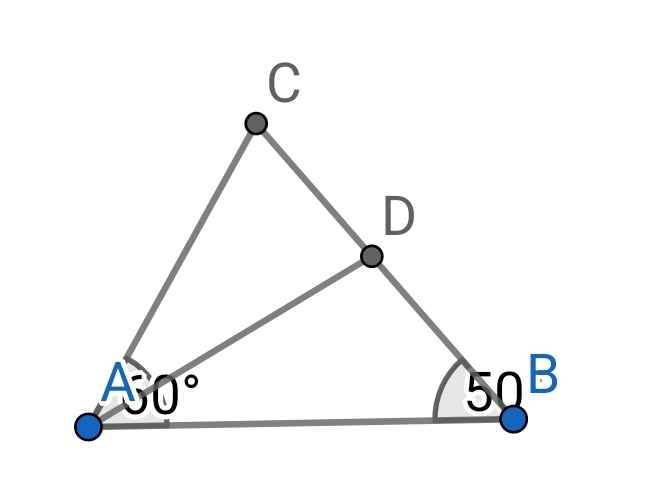 a) Do AD là tia phân giác của ∠BAC (gt)
a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠BAC : 2
= 60⁰ : 2
= 30⁰
∆ABD có:
∠BAD + ∠ABD + ∠ADB = 180⁰ (tổng ba góc trong ∆ABD)
⇒ ∠ADB = 180⁰ - ∠BAD - ∠ABD
= 180⁰ - 30⁰ - 50⁰
= 100⁰
b) Do 30⁰ < 50⁰ < 100⁰
⇒ ∠BAD < ∠ABD < ∠ADB
⇒ BD < AD < AB (quan hệ giữa cạnh và góc đối diện trong tam giác)

a)góc C=90-60=30 độ
CDE=90-DCE
BDE=90-DBE
DCE=DBE
suy ra CDE=BDE
xét 2 tam giác vuông DEC và DEB có:
DE(chung)
CDE=BDE(cmt)
CED=BED=90
suy ra tam giác DEC=DEB(g.c.g) suy ra CD=DB; DCE=CBD mà CBD=ABD suy ra DCE=DBA
xét 2 tam giác vuông ABD và EBD có:
DB=CD(cmt)
DBA=DCE(cmt)
suy ra tam giác ABD=EBD(GH-GN)
b) xét 2 tam giác vuông EDB và ADB có:
DB(chung)
DBA=EBD(gt)
suy ra tam giác EDB =ADB suy ra EB=AB mà B= 60 độ suy ra tam giác AEB đều
c)theo câu b, ta có: tam giác AEB đều suy ra EA=EB=AB=5cm
theo câu a, ta có: tam giác DEB= DEC(g.c.g) suy ra CE=EB =1/2BC suy ra BC=EB+EC=5x2=10(cm)