13. Đường thẳng EF cắt 2 đường thẳng AB và CD lần lượt tại M và N. Cho biết \(\widehat{AME}\) = \(3\widehat{EMB}\) và \(\widehat{AME}\) + \(\widehat{EMB}\) + \(\widehat{MND}\) = 225o. Xác định quan hệ giữa 2 đường thẳng AB và CD.
Gíup mình với cảm ơn các bạn...
Đọc tiếp
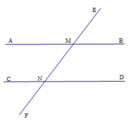
13. Đường thẳng EF cắt 2 đường thẳng AB và CD lần lượt tại M và N. Cho biết \(\widehat{AME}\) = \(3\widehat{EMB}\) và \(\widehat{AME}\) + \(\widehat{EMB}\) + \(\widehat{MND}\) = 225o. Xác định quan hệ giữa 2 đường thẳng AB và CD.
Gíup mình với cảm ơn các bạn nhiều!
\(\widehat{AMB}=\widehat{AME}+\widehat{EMB}=3\widehat{EMB}+\widehat{EMB}=4\widehat{EMB}=180^o\)
\(\Rightarrow\widehat{EMB}=180^o:4=45^o\)
Ta có
\(\widehat{AME}+\widehat{EMB}+\widehat{MND}=\widehat{AMB}+\widehat{MND}=225^o\)
\(\Rightarrow180^o+\widehat{MND}=225^o\Rightarrow\widehat{MND}=225^o-180^o=45^o\)
Gọi O là giao của AB và CD xét tg OMN có
\(\widehat{MON}=180^o-\left(\widehat{EMB}+\widehat{MND}\right)=180^o-\left(45^o+45^o\right)=90^o\)
\(\Rightarrow AB\perp CD\)
cảm ơn minh