Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với tốc độ ban đầu \({v_0} = 196m/s\) (bỏ qua sức cản của không khí). Tìm thời điểm tại đó tốc độ của viên đạn bằng 0. (lấy \(g = 9,8m/{s^2}\))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Chọn phương bắn là phương thẳng đúng theo trục Oy, chiều dương hướng từ dưới lên. Gốc O và vị trí viên đạn được bắn lên.
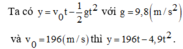
Vận tốc tức thời tại thời điểm t là
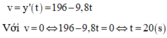
Lúc này viên đạn cách mặt đất một khoảng là
![]()

Đáp án B
Chọn phương bắn là phương thẳng đúng theo trục Oy, chiều dương hướng từ dưới lên. Gốc O và vị trí viên đạn được bắn lên.


Đáp án B
Ta có x = 400 t , y = 5 t 2 ; khi viên đạn rơi vào sườn đồi ta có y x = tan 30 0 = 1 3
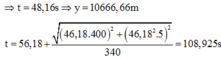

a) Thay g = 9,8 và \({v_0} = 500\)vào phương trình \(y = - \frac{g}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \) ta được
\(\begin{array}{l}y = - \frac{{9,8}}{{{{2.500}^2}.{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \\ = - \frac{1}{{{{\cos }^2}\alpha }}{.1,96.10^{ - 5}}.{x^2} + x\tan \alpha \\ = - \left( {1 + {{\tan }^2}\alpha } \right){1,96.10^{ - 5}}.{x^2} + x\tan \alpha \\ = x.\left[ {\tan \alpha - \left( {1 + {{\tan }^2}\alpha } \right){{.1,96.10}^{ - 5}}.x} \right]\end{array}\)
Khi đó y = 0
Suy ra x = 0 hoặc \(x = \frac{{\tan \alpha }}{{\left( {1 + {{\tan }^2}\alpha } \right){{.1,96.10}^{ - 5}}}}\)
Theo góc bắn \(\alpha \)tầm xa mà quả đạn đạt tới là \(\frac{{\tan \alpha }}{{\left( {1 + {{\tan }^2}\alpha } \right){{.1,96.10}^{ - 5}}}}\)
b) Quả đạn trúng mục tiêu cách vị trí đặt khẩu pháp 22 000 m thì x = 22 000 (m)
Khi đó
\(\begin{array}{l}22\,000 = \frac{{\tan \alpha }}{{\left( {1 + {{\tan }^2}\alpha } \right){{.1,96.10}^{ - 5}}}}\\ \Leftrightarrow 0,4312 = \frac{{\tan \alpha }}{{\left( {1 + {{\tan }^2}\alpha } \right)}}\\ \Rightarrow \alpha \approx {30^ \circ }\end{array}\)
( Bấm máy tính để tìm giá trị sấp xỉ của \(\alpha \))

Đáp án A
Chọn chiều dương là chiều hướng từ trên xuống dưới, gốc tọa độ tại vị trí viên bi A, gốc thời gian là lúc viên bi A rơi
Phương trình chuyển động :
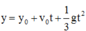
Phương trình chuyển động vật A :
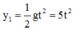
Phương trình chuyển động vật B:
![]()
![]()
Khi gặp nhau:
![]()
![]()
Suy ra t = 1,2s

a. Chọn chiều dương là chiều hướng từ trên xuống dưới, gốc tọa độ tại vị trí viên bi A, gốc thời gian là lúc viên bi A rơi
Phương trình chuyển động :

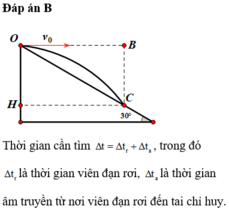

Cho Ox theo phương thẳng đứng, chiều hướng từ mặt đất lên trời, gốc O là vị trí viên đạn được bắn lên, khi đó phương trình chuyển động của viên đạn là: \(y = {v_0}t - \frac{1}{2}g{t^2}\,\,\left( {g = 9,8m/{s^2}} \right)\)
Ta có vận tốc tại thời điểm t là: \(v = y'\left( t \right) = {v_0} - gt\)
Do đó: \(v = 0 \Rightarrow {v_0} - gt = 0 \Leftrightarrow t = \frac{{{v_0}}}{g} = \frac{{196}}{{9.8}} = 20\,\,(s)\)