Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho Ox theo phương thẳng đứng, chiều hướng từ mặt đất lên trời, gốc O là vị trí viên đạn được bắn lên, khi đó phương trình chuyển động của viên đạn là: \(y = {v_0}t - \frac{1}{2}g{t^2}\,\,\left( {g = 9,8m/{s^2}} \right)\)
Ta có vận tốc tại thời điểm t là: \(v = y'\left( t \right) = {v_0} - gt\)
Do đó: \(v = 0 \Rightarrow {v_0} - gt = 0 \Leftrightarrow t = \frac{{{v_0}}}{g} = \frac{{196}}{{9.8}} = 20\,\,(s)\)

Đáp án C
Gọi A1 là biến cố viên thứ nhất trúng mục tiêu
Gọi A2 là biến cố viên thứ hai trúng mục tiêu
Do A1, A2 là hai biến cố độc lập nên xác suất để có một viên trúng mục tiêu và một viên trượt mục tiêu là
p = p ( A 1 A 2 ) + p ( A 1 A 2 ) = 0 , 6 . 0 , 4 + 0 , 4 . 0 , 6 = 0 , 48 .

Đáp án C
Có 2 trường hợp xảy ra là trúng – trượt và trượt – trúng
Xác suất cần tìm là 0,6.0,4 + 0,4.06 = 0,48

xác xuất bắn trượt là 1-0.6=0.4
xác xuất Tm bài toán 0.4*0.6=0.24

Gọi Ai là biến cố:” bắn viên đạn thứ i trúng mục tiêu”i=1,2,3
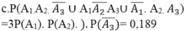
Chọn B

Gọi Ai là biến cố:” bắn viên đạn thứ i trúng mục tiêu”i=1,2,3
![]()
Chọn A
a) Thay g = 9,8 và \({v_0} = 500\)vào phương trình \(y = - \frac{g}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \) ta được
\(\begin{array}{l}y = - \frac{{9,8}}{{{{2.500}^2}.{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \\ = - \frac{1}{{{{\cos }^2}\alpha }}{.1,96.10^{ - 5}}.{x^2} + x\tan \alpha \\ = - \left( {1 + {{\tan }^2}\alpha } \right){1,96.10^{ - 5}}.{x^2} + x\tan \alpha \\ = x.\left[ {\tan \alpha - \left( {1 + {{\tan }^2}\alpha } \right){{.1,96.10}^{ - 5}}.x} \right]\end{array}\)
Khi đó y = 0
Suy ra x = 0 hoặc \(x = \frac{{\tan \alpha }}{{\left( {1 + {{\tan }^2}\alpha } \right){{.1,96.10}^{ - 5}}}}\)
Theo góc bắn \(\alpha \)tầm xa mà quả đạn đạt tới là \(\frac{{\tan \alpha }}{{\left( {1 + {{\tan }^2}\alpha } \right){{.1,96.10}^{ - 5}}}}\)
b) Quả đạn trúng mục tiêu cách vị trí đặt khẩu pháp 22 000 m thì x = 22 000 (m)
Khi đó
\(\begin{array}{l}22\,000 = \frac{{\tan \alpha }}{{\left( {1 + {{\tan }^2}\alpha } \right){{.1,96.10}^{ - 5}}}}\\ \Leftrightarrow 0,4312 = \frac{{\tan \alpha }}{{\left( {1 + {{\tan }^2}\alpha } \right)}}\\ \Rightarrow \alpha \approx {30^ \circ }\end{array}\)
( Bấm máy tính để tìm giá trị sấp xỉ của \(\alpha \))