Question

[Đào Trí Bình]

1. Cho tam giác ABC. Trên nửa mặt phẳng bờ AC ko chứa B vẽ tia Ax sao cho \(\widehat{xAC}\) = \(\widehat{ACB}\). Trên nửa mặt phẳng bờ AB ko chứa C vẽ tia Ay sao cho \(\widehat{yAB}\) = \(\widehat{ABC}\). Qua C kẻ đường thẳng d vuông góc với BC. Đường thẳng d có vuông góc với xy không? Vì sao?

Gíup mình giải bài này với!

Answer 1

[Nguyễn Xuân Thành]

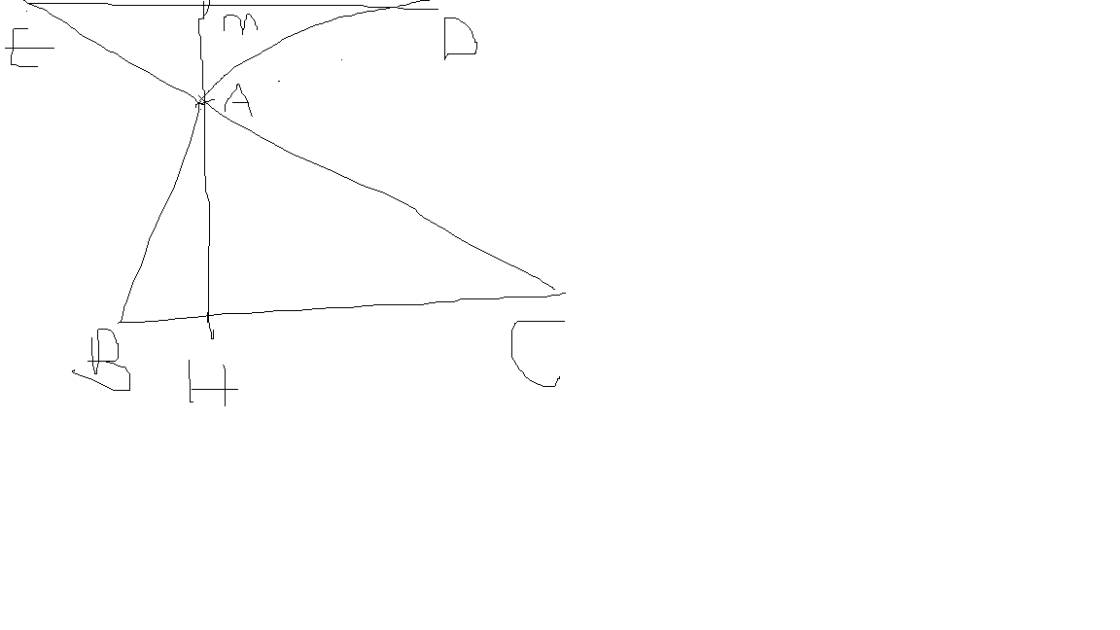
a) Ta có: $\widehat{CAx}=\widehat{ACB}\left(gt\right)$ mà hai góc đó là hai góc so le trong nên

suy ra $Ax//BC$ (1)

$\widehat{BAy}=\widehat{ABC}\left(gt\right)$ mà hai góc đó là hai góc so le trong nên suy ra $Ay//BC$ (2)

Từ (1) và (2) suy ra Ax và Ay cùng // BC.

Lại có tia Ax thuộc mặt phẳng bờ AB có chứa điểm C, tia Ay thuộc mặt phẳng

bờ  AB không chứa điểm C

$\Rightarrow$ Ax và Ay là hai tia đối nhau.

b) Vì Ax và Ay là hai tia đối nhau (cmt) mà $Ax//BC$ và $Ay//BC$

 nên suy ra $xy//BC$

Mà $BC\perp d$ nên suy ra $d\perp xy$